Numerical Modeling of Hydrogen Embrittlement-induced Ductile Fracture Using a Gurson-Cohesive Model (GCM) and Hydrogen Diffusion

Jihyuk Park; Nam-Su Huh; Kyoungsoo Park

doi:10.7734/COSEIK.2024.37.4.267

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 August 2024. 267-274
https://doi.org/10.7734/COSEIK.2024.37.4.267

Numerical Modeling of Hydrogen Embrittlement-induced Ductile Fracture Using a Gurson-Cohesive Model (GCM) and Hydrogen Diffusion

Gurson-Cohesive Model(GCM)과 수소 확산 모델을 결합한 수소 취화 파괴 해석 기법

Jihyuk Park¹

Nam-Su Huh²

Kyoungsoo Park³^†

박 지혁¹

허 남수²

박 경수³^†

¹Postdoctoral Researcher, Department of Civil & Environmental Engineering, Yonsei University, Seoul, 03722, Korea

²Professor, Department of Mechanical System Design Engineering, Seoul National University of Science and Technology, Seoul, 01811, Korea

³Professor, Department of Civil & Environmental Engineering, Yonsei University, Seoul, 03722, Korea

¹연세대학교 건설환경공학과 박사후연구원

²서울과학기술대학교 기계시스템디자인공학과 교수

³연세대학교 건설환경공학과 교수

^{†Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Hydrogen embrittlement fracture poses a challenge in ensuring the structural integrity of materials exposed to hydrogen-rich environments. This study advances our comprehension of hydrogen-induced fracture through an integrated numerical modeling approach. In addition, it employs a ductile fracture model named the Gurson-cohesive model (GCM) and hydrogen diffusion analysis. GCM is employed as a fracture model that combines the Gurson model to illustrate the continuum damage evolution and the cohesive zone model to describe crack surface discontinuity and softening behavior. Moreover, porosity and stress triaxiality are considered as crack initiation criteria . A hydrogen diffusion analysis is also integrated with the GCM to account for hydrogen enhanced decohesion (HEDE) mechanisms and their subsequent impacts on crack initiation and propagation. This framework considers the influence of hydrogen on the softening behavior of the traction–separation relationship on the discontinuous crack surface. Parametric studies explore the sensitivity to diffusion properties and hydrogen-induced fracture properties. By combining numerical models of hydrogen diffusion and the ductile fracture model, this study provides an understanding of hydrogen-induced fracture and thereby contributes significantly to the ongoing efforts to design materials that are resilient to hydrogen embrittlement in practical engineering applications.

Keywords

cohesive zone model

ductile fracture

hydrogen embrittlement fracture

hydrogen diffusion analysis

수소 취성 파괴는 수소가 풍부한 환경에 노출된 재료의 구조적 무결성을 보장하는 데 있어 다양한 산업 응용 분야에서 큰 도전 과제이다. 본 연구는 연성 파괴 모델인 Gurson-Cohesive 모델과 수소 확산 모델을 통합하는 수치 모델을 제안하고 수소 취화가 파괴 거동에 끼치는 영향을 조사한다. 사용된 연성 파괴 모델은 손상 진화를 모사하는 Gurson 모델과 균열 표면의 불연속성과 응력-균열폭 관계의 연화 거동을 설명하는 표면 요소 기반의 Cohesive zone 모델을 결합한 파괴 모델이며, 균열 시작 기준으로 공극과 삼축성을 고려한다. 또한, 파괴 모델과 통합된 수소 확산 분석은 수소 강화 탈결합(HEDE) 메커니즘과 그에 따른 균열 시작 및 진전에 미치는 영향을 고려하며, 응력-균열폭 관계에 대한 수소의 영향을 고려한다. 수치 예제로 매개변수 연구를 통하여 확산 계수와 수소 취화 파과 특성에 대한 민감도를 조사한다. 수소 확산 모델과 연성 파괴 모델을 통합한 프레임워크를 제시함으로써 본 연구는 수소 취화 파괴에 대한 이해를 제공하여 엔지니어링 응용 분야에서 기여할 수 있을 것이다.

키워드

Cohesive zone 모델

연성 파괴

수소 취화

수소 취화 파괴

수소 확산 분석

MAIN

1. 서 론
2. 수소 파괴 해석 모델
2.1 Gurson-Cohesive model
2.2 수소 확산 모델
2.3 파괴 해석과 확산 해석의 결합
3. 파괴 인성 시험을 이용한 매개변수 연구
4. 결 론

1. 서 론

수소 취화는 금속이 수소에 노출될 때 연성, 강도 및 파괴 인성이 저하되는 현상이다. 이는 수소를 화석 연료 대체 에너지원으로 사용하는 운송 및 저장 장치뿐만 아니라 연료 및 가스의 배관 등에서 흔히 발생하는 현상이다(Cha et al., 2022). 이러한 수소 취화 현상을 설명하기 위해 다양한 메커니즘 및 이론이 제안되었다(Li et al., 2020). 여기에는 Hydrogen-Enhanced DEcohesion(HEDE) 매커니즘, Hydrogen-Enhanced Localized Plasticity(HELP) 매커니즘, hydrogen-enhanced strain-induced vacancies(HESIV) 매커니즘, hydrogen pressure 이론, hydrogen-induced phase transformation 이론 등이 포함된다. 이러한 메커니즘은 미세 스케일(HEDE)부터 나노 스케일(HELP, HESIV)까지 다양한 스케일에서 수소 취화를 설명한다. 특히 HEDE 매커니즘은 수소 원자가 금속 내의 결합 강도를 약화시켜 균열이 발생하는 메커니즘으로, 수소가 재료의 강도를 저하시켜 파괴를 유발하는 과정을 모사하는 매커니즘이다(Serebrinsky et al., 2004).

수소 취화 파괴는 복잡한 응력-확산 현상으로 다양한 차원에서 여러 목적으로 연구되고 있다. 특히 Dugdale(Dugdale, 1960)이 제안한 Cohesive zone 모델은 수소 환경에서 금속의 기계적 특성 저하를 매크로 스케일에서 예측하는 일반적인 수치 기법이다. Cohesive zone 모델의 주요 특징은 균열 진전 영역에서 연속체 요소와 연결된 Cohesive 요소로 균열을 표현하며, traction-separation 관계를 통해 손상을 추정할 수 있다. 최근 cohesive 강도 및 파괴에너지 등을 조정하여 수소 취화에 의한 손상 및 파괴를 거동을 모사하는 기법들이 제안되었다(Dwivedi and Vishwakarma, 2018; Gobbi et al., 2019; Huang et al., 2023; Lin et al., 2022).

본 논문에서는 Gurson 모델과 Cohesive zone 모델을 사용한 연성 파괴 모델(Park et al., 2024c)과 일반적인 수소 확산 모델을 HEDE 메커니즘을 고려하여 결합한 수소 취화 파괴 모델을 제안한다. 또한, 사용된 연성 파괴 모델 특성 중 하나인 공극 기반 균열 발생 기준을 이용하여 Cohesive 강도의 저감 대신 임계 공극의 저감을 통해 수소 취화에 의한 균열 발생 및 진전을 모사한다. 연성 파괴 모델을 사용하여 응력, 변형률 및 손상을 구하고 계산된 응력과 변형률을 사용하여 확산 해석을 진행한다. 다양한 수소 취화 매커니즘 중 HEDE 매커니즘을 고려하여 확산 해석을 통해 구한 수소 농도로부터 수소 취화 계수를 평가하고 이를 이용하여 국소적으로 균열 발생 기준과 파괴에너지를 저감한 후 표면 요소로 나타내어지는 Cohesive zone 모델을 연속체 계면에 삽입하여 균열 발생 및 진전을 모사한다.

2. 수소 파괴 해석 모델

이 장에서는 수소취화 파괴 해석 프레임워크에 사용된 파괴모델과 수소확산모델을 소개한 후, 결합 방식에 대하여 설명하고자 한다.

2.1 Gurson-Cohesive model

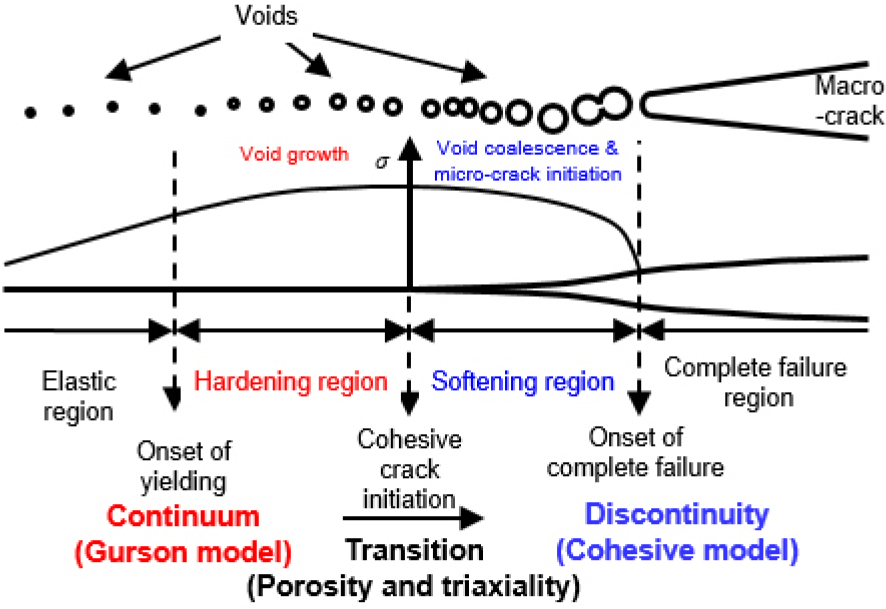
연속체 손상과 비선형 파괴 과정을 모사하기 위해 손상 모델중 하나인 Gurson 모델과 Cohesive zone 모델을 통합한 연성 파괴 모델인 Gurson-Cohesive 모델(GCM)이 사용되었다(Park et al., 2024c). GCM은 연성 파괴 과정을 네 단계(탄성, 경화, 연화, 완전 파괴)로 구분한다(Fig. 1). 초기에는 재료가 탄성 단계에 있으며, 응력과 변형률이 증가하면서 재료가 항복하고, 경화 단계로 넘어오게 된다. 이 단계에서는 Gurson 모델(Gurson, 1977)을 사용하여 항복의 시작과 경화 단계의 재료 반응 및 공극의 성장을 정의한다. 공극 합체와 미세 균열이 발생하면 연화 단계가 시작되며, 이때 연화 단계로의 전환은 공극 기반의 균열 시작 기준을 도입하여 정의된다. 연화 단계는 PPR traction-separation 관계(Park et al., 2009)와 결합된 Cohesive zone 모델로 설명된다. Cohesive 분리가 완전 파괴 분리보다 클 때는, 균열 표면을 따라 응력이 지탱할 수 없으며 완전 파괴 거동을 한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370406/images/Figure_jcoseik_37_04_06_F1.jpg

Fig. 1.

Schematics of the ductile fracture process in GCM

연속체의 거동을 모사함에 있어 사용된 Gurson 모델의 항복 표면은 다음 식 (1)로 표현된다(Gurson, 1977).

(1)

F (σ) = \frac{σ_{e q}^{2}}{σ_{y}^{2}} + 2 f \cosh (\frac{3}{2} \frac{σ_{H}}{σ_{y}}) - (1 + f^{2})

여기서, $f$ 와 $σ_{y}$ 는 공극과 항복응력을 나타내며, $σ_{e q} = \sqrt{3 / 2 σ' : σ'}$ 와 $σ_{H} = t r (σ) / 3$ 은 Von Mises 응력과 정수압 응력을 나타내고 각각 응력( $σ$ )과 편차응력( $σ'$ )으로 구할 수 있다. 항복응력은 등가소성변형률( ${\bar{ϵ}}^{p}$ )에 대한 함수로 나타낼 수 있으며,

(2)

σ_{y} = σ_{s} (1 + {\bar{ϵ}}^{p} / ϵ_{0})^{N}

$σ_{s}$ , $N$ , 와 $ϵ_{0}$ 는 재료 상수이다. 소성 변형률 속도( ${\dot{E}}^{p}$ )는 항복 표면의 법선 방향과 소성 배수(𝜆)의 식으로 다음 식 (3)과 같이 주어진다.

(3)

{\dot{E}}^{p} = \dot{λ} \frac{\partial F}{\partial σ}

연속체 요소의 소성 변형률의 일( $σ : {\dot{E}}^{p}$ )은 공극을 제외한 매트릭스의 등가소성변형률의 일과 같으며,

(4)

σ : {\dot{E}}^{p} = (1 - f) σ_{y} {\dot{\bar{ϵ}}}^{p}

공극의 성장은 소성비압축성에 대한 식 (5)로 나타난다.

(5)

\dot{f} = (1 - f) t r ({\dot{E}}^{p}) = (1 - f) \dot{λ} \frac{\partial F}{\partial σ_{H}}

비선형 파괴 과정 영역은 경화 영역과 불연속 파괴 표면을 연결하며, 이는 재료의 연화 반응과 관련이 있다. 비선형 파괴 과정은 extrinsic PPR Cohesive zone 모델(Park et al., 2009)을 사용하여 정의된다. PPR 모델에서 파괴 잠재력(Ψ)은 다음과 같이 주어진다.

(6)

Ψ (Δ_{n}, Δ_{t}) = \min (ϕ_{n}, ϕ_{t}) + [Γ_{n} {(1 - \frac{Δ_{n}}{δ_{n}})}^{α} + < ϕ_{n} - ϕ_{t} >] [Γ_{t} {(1 - \frac{| Δ_{t} |}{δ_{t}})}^{β} + < ϕ_{t} - ϕ_{n} >]

여기서, $Δ_{n}$ 와 $Δ_{t}$ 는 각각 법선과 접선 방향으로의 완전 바괴 분리 값이고 $< ∙ >$ 는 Macauley 브래킷이다. 식 (6)에서 사용되는 매개변수( $Γ_{n}$ , $Γ_{t}$ , $δ_{n}$ , $δ_{t}$ )는 파괴 에너지( $ϕ_{n}$ , $ϕ_{t}$ ), Cohesive 강도( $σ_{\max}$ , $τ_{\max}$ ), 형상 변수(𝛼,𝛽)를 이용하여 계산한다(Park et al., 2009; Park and Paulino, 2012). 식 (6)을 $Δ_{n}$ 와 $Δ_{t}$ 로 미분하여 Cohesive 모델에서의 traction-separation 관계를 얻을 수 있다.

(7)

T_{n} (Δ_{n}, Δ_{t}) = \partial Ψ (Δ_{n}, Δ_{t}) / \partial Δ_{n}

(8)

T_{t} (Δ_{n}, Δ_{t}) = \partial Ψ (Δ_{n}, Δ_{t}) / \partial Δ_{t}

연속체 손상에서 불연속 균열으로 전이는 균열 발생기준을 사용하여 판단한다. 전이의 시작은 공극과 삼축 응력(𝜂)을 고려한 배수 공극( $f_{η}$ )이 임계 공극( $f_{c r}$ )을 초과하게 되면 Cohesive 요소를 삽입하여 균열의 발생을 표현한다. 배수 공극은 다음 식 (9)로 나타내어진다.

(9)

f_{η} = f ⟨ η ⟩^{m} H (∆ f)

여기서, 𝜂은 삼축 응력 상태를 나타내고, m은 재료 상수이다. Macauley 브래킷은 삼축 응력이 음수일 경우를 피하기 위하여 사용되었고 $H (∙)$ 은 공극의 성장하는 경우만을 고려하기 위하여 사용되었다. 임계 공극의 크기가 작아지거나 m의 크기가 커질수록 균열 선단에서(삼축 응력 상태가 양수이므로) 균열의 발생이 더 가속화된다.

연성 파괴 모델의 유한요소법을 이용한 시뮬레이션을 위하여 다음과 같은 방법들을 사용하였다(Park et al., 2024a; 2024b). 연속체의 비선형 거동은 logarithmic 변형률과 updated Lagrangian 방법을 이용해 시간 적분을 하여 모사하였고, 재료의 큰 변형은 Jaumann 응력을 사용함으로써 고려하였다. 또한 균열 발생 및 진전은 Mode-I 균열을 가정하여 잠재적 균열 경로에서만 발생한다고 가정한 후, 경로 내의 균열 발생 조건을 만족하는 요소 경계면에 Cohesive 표면 요소를 삽입함으로써 균열 발생 및 진전을 모사하였다.

2.2 수소 확산 모델

본 연구에서는 문헌에서 일반적으로 사용되는 가정을 채택하고(Di Leo and Anand, 2013; Sofronis and McMeeking, 1989), Oriani가 제시한 평형 이론을 바탕으로 모델링을 진행한다(Oriani and Josephic, 1974). 수소 원자는 정상 간극 격자 위치(Normal interstitial lattice site)를 차지할 수 있으며, 추가로 계면이나 전위와 같은 트랩 위치(Trap site)에 머무를 수 있다. 간극 격자 위치에서의 수소 농도( $C_{L}$ )와 미세 구조 결함에 갇힌 트랩 위치의 수소 농도( $C_{T}$ )는 다음 식 (10), (11)과 같이 표현된다.

(10)

C_{L} = θ_{L} N_{L}

(11)

C_{T} = θ_{T} N_{T}

여기서, $θ_{L}$ 와 $N_{L}$ 은 각각 격자 점유율과 용매 원자 단위 부피당 측정된 호스트 금속 격자의 밀도를 나타내고, $θ_{T}$ 와 $N_{T}$ 는 각각 트랩 점유율과 단위 부피당 트랩의 수를 나타낸다. 본 연구에서는 단위 부피당 트랩의 수를 결함 밀도(𝜌)에 대한 관계식으로 나타낸다(Sofronis et al., 2001).

(12)

N_{T} = \frac{1}{b} ρ

여기서, $b$ 는 격자 파라메터이고 결함 밀도는 등가소성변형률에 대한 식 (13)으로 나타낸다.

(13)

ρ = \{\begin{cases} ρ_{0} + γ {\bar{ϵ}}^{p} for {\bar{ϵ}}^{p} < 0.5 \\ ρ_{1} for {\bar{ϵ}}^{p} > 0.5 \end{cases}

여기서, $ρ_{0}$ , $ρ_{1}$ 와 $γ$ 의 값은 각각 1.0 × 10¹⁰m/m³, 1.0 × 10¹⁶m/m³와 2.0 × 10¹⁶m/m³이다.

격자와 트랩의 점유율 간의 관계는 Orinai의 평형 이론(Oriani and Josephic, 1974)으로 나타낼 수 있으며,

(14)

\frac{θ_{T}}{1 - θ_{T}} = \frac{θ_{L}}{1 - θ_{L}} K

평형상수 $K$ 는 수소 원자가 트랩 사이트에서 벗어나 격자 사이트로 이동하는 데 필요한 에너지( $W_{B}$ )에 대한 함수이며, 식 (15)으로 계산할 수 있다.

(15)

K = \exp (- \frac{W_{B}}{R T})

격자와 트랩의 점유율 관계식을 이용하여 트랩의 농도를 격자의 농도에 대한 식으로 다음 식 (16)과 같이 표현할 수 있다.

(16)

C_{T} = \frac{K C_{L} N_{T}}{N_{L} + C_{L} (K - 1)}

확산 해석 수행에 있어 수소의 총 농도( $C = C_{L} + C_{T}$ )에 대한 방정식은 다음과 같으며,

(17)

\frac{d C}{d t} - \nabla ∙ J = 0

수소의 플럭스는 Fick의 법칙을 사용하여 나타낸다.

(18)

J = - D \nabla C_{L} + \frac{D}{R T} C_{L} {\bar{V}}_{H} \nabla σ_{H}

여기서, $D$ 와 ${\bar{V}}_{H}$ 는 각각 확산 계수와 부분 질량 부피이고 $R$ 과 $T$ 는 각각 기체상수와 현재 온도이다. 식 (17)을 사용한 weak formulation은 식 (19)로 나타낼 수 있고 incremental form으로 변환 후 유한요소법을 통하여 해를 찾는다(Park et al., 2024a).

(19)

\int_{Ω} δ C_{L} \frac{d C}{d t} d Ω + \int_{Γ} δ C_{L} n ∙ J d Γ - \int_{Ω} \nabla δ C_{L} ∙ J d Ω = 0

2.3 파괴 해석과 확산 해석의 결합

본 연구에서는 HEDE 매커니즘을 고려하여 응력 및 파괴 해석과 수소 확산 해석을 결합하여 수소 취화 파괴 해석을 수행한다. HEDE 매커니즘에서 수소가 금속 원자 간 결합 강도와 결합의 분리에 대한 저항을 감소시키는 현상(Li et al., 2020; Serebrinsky et al., 2004)을 고려하여 파괴 에너지를 저감시키고 수소 취화가 진행됨에 따라 파괴 단면의 공극이 줄어드는 현상(Tiwari et al., 2000)을 고려하여 임계 공극을 저감시켰다.

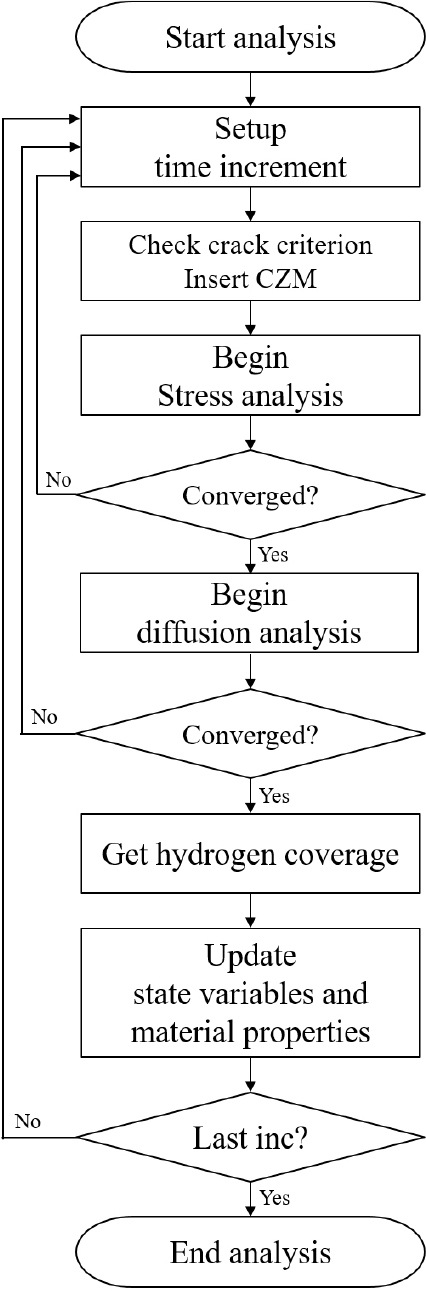
해석의 알고리즘은 Fig. 2와 같다. 먼저 해당 시간 증분 단계에 대한 응력 및 파괴해석을 진행한 후, 변형률과 응력을 이용해서 수소 확산 해석을 진행한다. 확산 해석 후 계산된 수소 농도를 이용하여 국부적 임계 공극과 잠재적 Cohesive 요소의 파괴에너지를 저감 계수( $k$ )를 사용하여 저감한다. 저감 계수는 표면 수소 농도를 이용한 식을 이용하였다(Serebrinsky et al., 2004).

표면 수소 농도와 포화 농도의 비(𝜃)는 다음 식 (20)을 이용하여 계산한다.

(20)

θ = \frac{C}{C + \exp (- ∆ g_{b} / R T)}

여기서, $∆ g_{b}$ 는 깁스 에너지이다. 저감 계수 값은 다음 경험식 (21)을 이용한다.

(21)

k = 1 - 1.0467 θ + 0.1687 θ^{2}

이때, 저감된 임계 공극과 파괴 에너지는 각각 식 (22), (23)으로 나타낼 수 있다.

(22)

(f_{c r})_{H} = k \times f_{c r}

(23)

(ϕ_{n})_{H} = k \times ϕ_{n}

저감 계수의 범위는 $0.122 < k < = 1$ 이고, 재료 내부에 수소가 없을 때 $k = 1$ 이 되고 파괴 에너지 및 임계 공극은 감소하지 않는다. 그 후 새로운 시간 증분 단계에서 배수 공극이 임계 공극보다 크면 Cohesive 표면 요소를 삽입하여 균열의 발생 혹은 진전시키고 해당 Cohesive 요소의 파괴 에너지는 식 (23)로 계산된 값으로 설정한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370406/images/Figure_jcoseik_37_04_06_F2.jpg

Fig. 2.

Algorithm of hydrogen embrittlement-induced fracture analysis

3. 파괴 인성 시험을 이용한 매개변수 연구

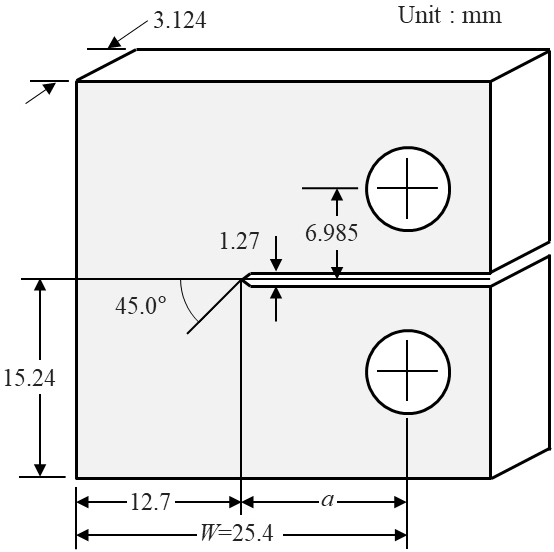
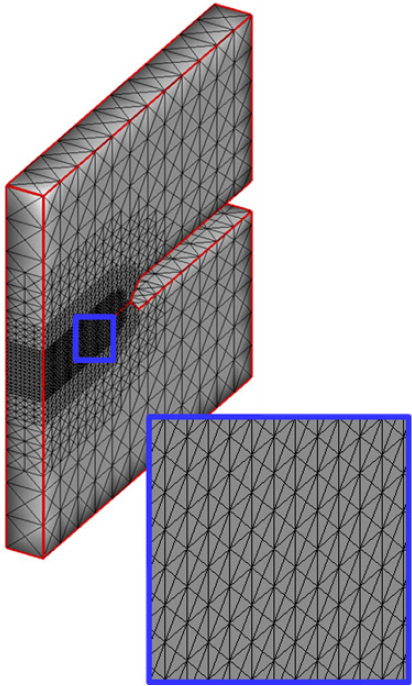
이 논문에서 제시한 수소 취화 파괴 해석을 이용한 파괴 거동의 매개변수의 민감도 분석을 위하여 파괴 인성 실험을 이용하여 매개변수 연구를 수행하였다. 시편의 구성은 Fig. 3과 같고 해석에 이용된 요소망은 4-절점 사면체 요소를 이용하였다(Fig. 4). 사용된 요소망의 최소 요소의 크기는 0.2mm이고 총 요소와 절점의 개수는 각각 343,896개와 74,537개이다. 해석에 사용된 재료 물성치와 매개변수들은 Table 1에 요약하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370406/images/Figure_jcoseik_37_04_06_F3.jpg

Fig. 3.

Geometry of compact tension test

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370406/images/Figure_jcoseik_37_04_06_F4.jpg

Fig. 4.

Finite mesh for compact tension test

Table 1.

Material properties for parametric study

Model	Variables	unit	Value
GCM: Continuum	$f_{0}$	-	0.005
	$σ_{s}$	MPa	1030
	$ϵ_{0}$	-	0.005
	$N$	-	0.16
GCM: Crack initiation criterion	$f_{c r}$	-	0.008
GCM: Crack initiation criterion	$m$	-	1
GCM: Cohesive zone	$ϕ_{n}$	N/mm	250
GCM: Cohesive zone	$α$	-	2
Diffusion	$T$	K	300
	$∆ g_{b}$	kJ/mol	30
	${\bar{V}}_{H}$	mm³/mol	2000
	$N_{L}$	site/mm³	5.1 × 10¹³
	$W_{B}$	J/mol	20.2 × 10⁶
	$b$	Å	2.725
	$D$	mm²/sec	1.271 × 10^-3 - 1.271 × 10^-1
	$C_{0}$	atom/mm³	5.0 × 10¹¹ - 5.0 × 10²³

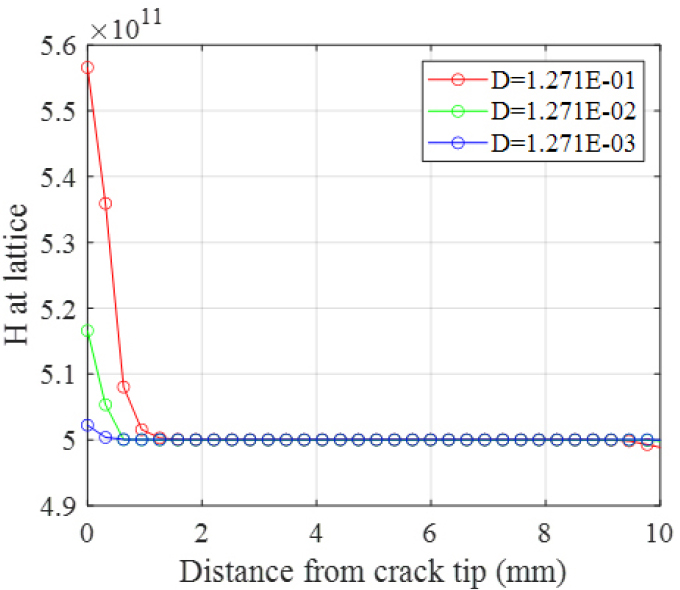
먼저 제시한 모델의 삼축 응력의 공간 기울기에 따른 농도를 확인하기 위하여 균열 발생 직전 잠재적 균열 경로의 격자 내 농도 분포를 확인하였다. 시편의 경계면은 모두 단열되어 있다고 가정하였고 수소의 확산은 응력 분포에 의해서만 일어나도록 하였다. Fig. 5는 균열 발생 직전 잠재적 균열 경로의 격자 내 수소 농도 분포에 대한 그래프이다. 서로 다른 확산 계수 결과 모두 상대적으로 응력이 큰 균열 선단에선 수소의 농도가 크게 분포되는 것을 확인할 수 있다. 확산 계수를 1.271 × 10^-3부터 1.271 × 10^-1mm²/sec까지 변화시켜 해석한 결과 확산 계수가 클수록 균열 선단의 수소 농도가 더 크게 집중되는 것을 확인할 수 있었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370406/images/Figure_jcoseik_37_04_06_F5.jpg

Fig. 5.

Finite mesh for compact tension test

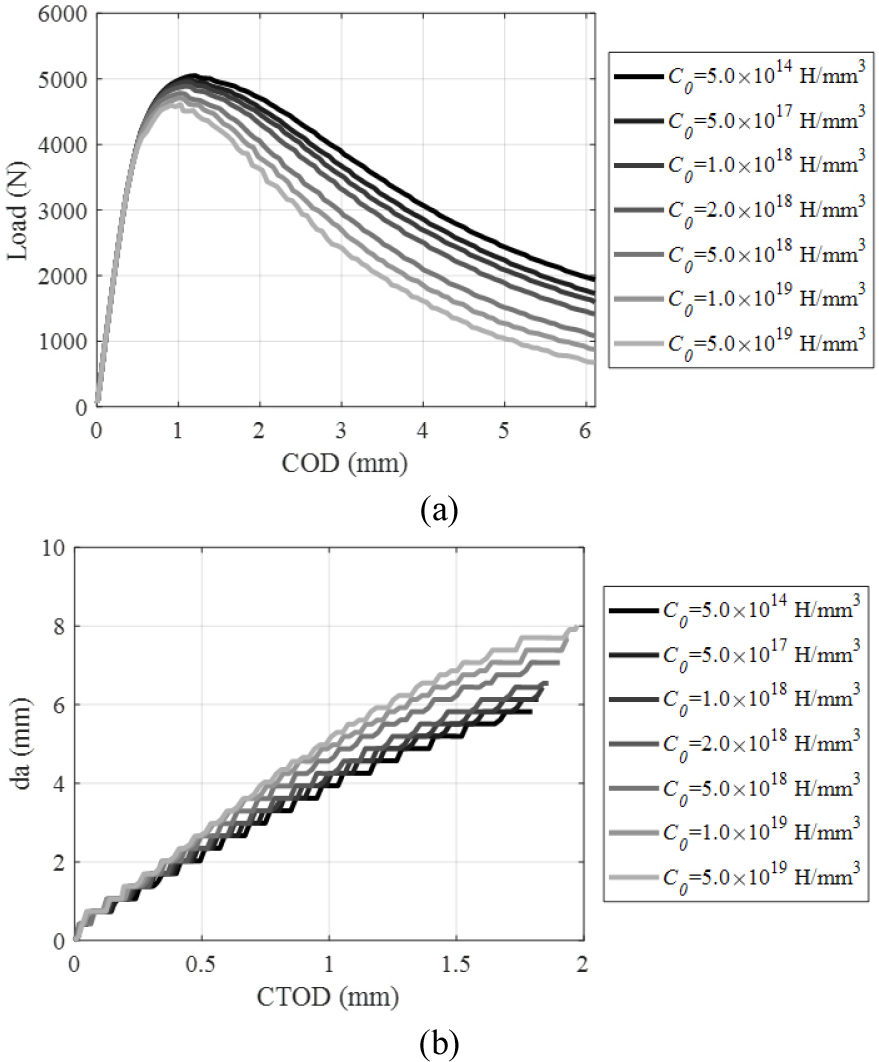
다음은 초기 수소농도의 시편의 파괴거동에 대한 영향을 조사하였다. 먼저 HEDE 매커니즘에서 수소가 금속 원자 간 결합 강도와 결합의 분리에 대한 저항을 감소시키는 현상만을 고려하여 Cohesive 요소의 파괴에너지를 식 (22)를 사용하여 감소시켰다. 초기 농도는 5.0 × 10¹⁴부터 5.0 × 10¹⁹atom/mm³까지의 값을 변화시켜 해석을 수행하였다. 하중-COD(Crack opening displacement, 균열 개구 변위) 곡선과 da(균열 길이)-CTOD(Crack tip opening displacement, 균열 선단 개구 변위)의 결과는 각각 Fig. 6(a)와 (b) 그림과 같다. 초기 수소 농도가 높아질수록 삽입되는 Cohesive 요소의 파괴 에너지가 감소하게 되므로 파괴 거동에 있어서 최대 하중이 점점 감소하고 CTOD 대비 균열 길이도 증가하는 것을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370406/images/Figure_jcoseik_37_04_06_F6.jpg

Fig. 6.

Results of reducing only fracture energy: (a) Load-COD curves and (b) da-CTOD curves

해석 결과는 Table 2에 요약되어 있다. 수소의 초기 농도가 5.0 × 10¹⁴atom/mm³일 때(No.1-1), 최대 하중이 5.048kN인 반면에 초기 농도가 5.0 × 10¹⁹atom/mm³일 때(No.1-7), 최대 하중은 4.609kN으로 No.1-1에 비해서 8.7% 감소하였다. 하중-COD 곡선의 면적(Work area)의 경우 No.1-7은 No.1-1에 비하여 31.0%나 감소하였다. 다음은 CTOP의 값이 0.25mm일 때의 da 값을 사용하여 da-CTOD 곡선의 초기 기울기를 구하였다. No.1-1 경우 초기 기울기가 5.378mm/mm이고 No.1-7에는 초기 기울기가 5.513mm/mm까지 증가하였다.

Table 2.

Results summary of reducing only fracture energy

No.	Initial concentration (atom/mm³)	Peak load (kN)	Work area (kN×mm)	da-CTOD slope (mm/mm)
1-1	5 × 10¹⁴	5.048	21.287	5.378
1-2	5 × 10¹⁷	4.993	20.335	5.618
1-3	1 × 10¹⁸	4.952	19.683	5.522
1-4	2 × 10¹⁸	4.887	18.772	5.395
1-5	5 × 10¹⁸	4.782	17.085	5.604
1-6	1 × 10¹⁹	4.712	15.883	5.526
1-7	5 × 10¹⁹	4.609	14.682	5.513

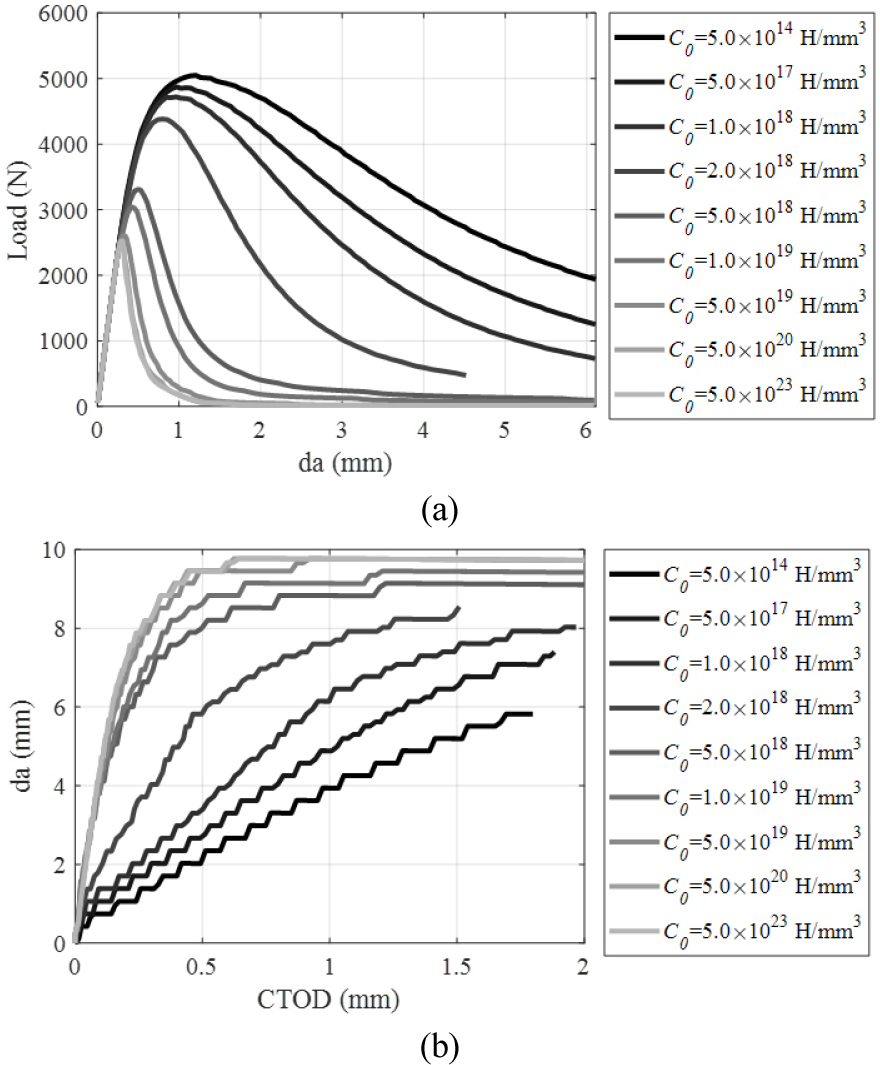
HEDE 매커니즘에서 수소가 금속 원자 간 결합 강도와 결합의 분리에 대한 저항을 감소시키는 현상과 수소 취화가 진행됨에 따라 파괴 단면의 공극이 줄어드는 현상을 모두 고려하여 해석을 진행하였다. Coheisve 파괴 에너지와 임계 공극은 각각 식 (22)과 (23)를 사용하여 감소시켰다. 초기 농도는 5.0 × 10¹⁴부터 5.0 × 10²³atom/mm³까지의 값을 변화시켰다. Fig. 7(a)와 (b)는 각각 하중-COD 곡선과 da-CTOD 곡선이다. Fig. 7(a)에서 초기 수소 농도가 증가할수록 최대 하중이 크게 감소하고, 최대 하중 이후 하중 감소의 기울기가 커지는 것을 확인할 수 있다. 이는 Fig. 6(a)에서 파괴 에너지만 저감시킨 결과와 차이가 있다. 또한, Fig. 7(b)에서 CTOD 대비 균열 길이 증가량도 초기 수소 농도에 따라 파괴 에너지만 저감시킨 결과(Fig. 6(b))보다 큰 것을 확인할 수 있다. 초기 수소 농도가 높은 경우 CTOD 값이 증가함에 따라 상대적으로 빠르게 균열 선단이 시편의 경계에 도달하면서 하중이 0kN에 가까워진 후 균열 길이의 증가량이 감소함을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370406/images/Figure_jcoseik_37_04_06_F7.jpg

Fig. 7.

Results of reducing fracture energy and critical porosity: (a) Load-COD curves and (b) da-CTOD curves

해석 결과는 Table 3에 요약되어 있다. 수소의 초기 농도가 5.0 × 10¹⁴atom/mm³일 때(No.2-1), 최대 하중이 5.048kN 인 반면에 초기 농도가 5.0 × 10¹⁹atom/mm³일 때(No.2-7)와 5.0 × 10²³atom/mm³일 때(No.2-9), 최대 하중은 각각 2.606kN과 2.521kN으로 No.2-1에 비해서 각각 48.4%와 50.0% 감소하였다. 이는 No.1-7의 최대하중이 No.1-1의 최대하중에서 8.7% 감소한 수치보다 더 크게 감소한 수치이다. Work area의 경우 또한 No.2-7은 No.2-1에 비하여 93.4%나 감소하였다. 이는 시편이 파괴될 필요한 에너지가 대부분 감소되었다고 할 수 있다. da-CTOD 곡선의 초기 기울기는 No.2-9의 경우 30.981mm/mm까지 증가하였으며 No.2-1의 초기 기울기 5.38mm/mm에 비하여 균열의 진전 속도가 5.8배 빠르다 할 수 있다.

Table 3.

Results summary of reducing fracture energy and critical porosity

No.	Initial concentration (atom/mm³)	Peak load (kN)	Work area (kN×mm)	da-CTOD slope (mm/mm)
2-1	5 × 10¹⁴	5.048	21.287	5.378
2-2	5 × 10¹⁷	4.872	18.086	6.974
2-3	1 × 10¹⁸	4.719	15.022	8.306
2-4	2 × 10¹⁸	4.383	8.993	14.688
2-5	5 × 10¹⁸	3.307	3.857	25.132
2-6	1 × 10¹⁹	3.044	2.701	26.720
2-7	5 × 10¹⁹	2.606	1.415	30.931
2-8	5 × 10²⁰	2.531	1.105	31.388
2-9	5 × 10²³	2.521	1.072	30.981

4. 결 론

본 연구에서는 연성 파괴 해석과 수소 확산 해석을 결합한 수소 취화파괴 해석 기법을 제안하였다. 연성 파괴 해석으로 Gurson모델과 Cohesive zone 모델을 결합하여 연속체의 손상 및 불연속 균열 거동을 모사하는 Gurson-Cohesive 모델을 사용하였고 수소 확산 해석으로 격자 및 트랩 위치의 수소 확산을 고려한 Fick 법칙을 사용하였다. 확산 해석을 통한 수소 농도에 따라 균열 진전을 나타내는 Cohesive 요소의 파괴 에너지와 균열 발생 기준으로 사용되는 임계 공극을계산하였다. 수치예로 파괴 인성 시험을 이용하여 확산 계수의 영향, 초기 농도의 영향, 파괴 에너지와 임계 공극의 저감에 대하 연구를 수행하였다.

확산 계수에 따른 균열 발생 전 수소 농도의 분포 결과를 통해, 균열 선단에서 응력 집중에 따른 수소 농도의 집중이 확산 계수가 클수록 더 크게 일어나는 것을 확인하였고, 확산 계수의 크기에 따라 수소 취화 과정이 가속화 될 수 있음을 확인하였다. 또한 초기 수소 농도의 증가가 시편의 전체적인 파괴 인성을 감소시키는 것을 확인하였고, 파괴 에너지 감소보다 임계 공극의 감소가 최대 하중 및 Work area를 더 크게 감소시키고 균열 진전 속도를 더 크게 가속시킨다는 것을 확인하였다.

Acknowledgements

본 연구는 한국과학재단이 주관하는 중견연구자지원사업(2022R1A2C2010081)의 지원을 받아 수행되었습니다.

References

Cha, S.H., Kim, H.S., Cho, S. (2022) Parametric Studies on Hydrogen Embrittlement in Liquified Hydrogen Tank using Molecular Dynamics Simulation, J. Comput. Struct. Eng. Inst. Korea, 35(6), pp.325~331.

10.7734/COSEIK.2022.35.6.325

Di Leo, C.V., Anand, L. (2013) Hydrogen in Metals: a Coupled Theory for Species Diffusion and Large Lastic-Plastic Deformations, Int. J. Plast., 43, pp.42~69.

10.1016/j.ijplas.2012.11.005

Dugdale, D.S. (1960) Yielding of Steel Sheets Containing Slits, J. Mech. Phys. Solids, 8(2), pp.100~104.

10.1016/0022-5096(60)90013-2

Dwivedi, S.K., Vishwakarma, M. (2018) Hydrogen Embrittlement in Different Materials: A Review, Int. J. Hydrog. Energy., 43(46), pp.21603~21616.

10.1016/j.ijhydene.2018.09.201

Gobbi, G., Colombo, C., Miccoli, S., Vergani, L. (2019) A fully coupled implementation of hydrogen embrittlement in FE analysis, Adv. Eng. Softw., 135, p.102673.

10.1016/j.advengsoft.2019.04.004

Gurson, A.L. (1977) Continuum Theory of Ductile Rupture by Void Nucleation and Growth, J. Eng. Mater. Technol., 99, pp.2~15.

10.1115/1.3443401

Huang, S., Hui, H., Peng, J. (2023) Prediction of Hydrogen-Assisted Fracture under Coexistence of Hydrogen-Enhanced Plasticity and Decohesion, Int. J. Hydrog. Energy, 48(94), pp.36987~37000.

10.1016/j.ijhydene.2023.06.033

Li, X., Ma, X., Zhang, J., Akiyama, E., Wang, Y., Song, X. (2020) Review of Hydrogen Embrittlement in Metals: Hydrogen Diffusion, Hydrogen Characterization, Hydrogen Embrittlement Mechanism and Prevention, Acta Metall. Sin. (Engl. Lett.), 33, pp.759~773.

10.1007/s40195-020-01039-7

Lin, M., Yu, H., Wang, X., Wang, R., Ding, Y., Alvaro, A., Olden, V., Zhang, Z. (2022) A Microstructure Informed and Mixed-Mode Cohesive Zone Approach to Simulating Hydrogen Embrittlement, Int. J. Hydrog. Energy, 47(39), pp.17479~17493.

10.1016/j.ijhydene.2022.03.226

Oriani, R.A., Josephic, P.H. (1974) Equilibrium Aspects of Hydrogen-induced Cracking of Steels, Acta Metall., 22(9), pp.1065~1074.

10.1016/0001-6160(74)90061-3

Park, J., Huh, N.S., Park, K. (2024a) Numerical Modeling of Hydrogen Embrittlement Fracture with Hydrogen Diffusion Model and Gurson-Cohesive Model. (in preparation)

Park, J., Kweon, S., Park, K. (2024b) Computational Implementation of Gurson-Cohesive Modeling and Its Applications. (in preparation)

Park, J., Kweon, S., Park, K. (2024c) Gurson-Cohesive Modeling (GCM) for 3D Ductile Fracture Simulation, Int. J. Plast., p.103914.

10.1016/j.ijplas.2024.103914

Park, K., Paulino, G.H. (2012) Computational Implementation of the PPR Potential-based Cohesive Model in ABAQUS: Educational Perspective, Eng. Fract. Mech., 93, pp.239~262.

10.1016/j.engfracmech.2012.02.007

Park, K., Paulino, G.H., Roesler, J.R. (2009) A Unified Potential-based Cohesive Model of Mixed-Mode Fracture, J. Mech. Phys. Solids, 57, pp.891~908.

10.1016/j.jmps.2008.10.003

Serebrinsky, S., Carter, E.A., Ortiz, M. (2004) A Quantum-Mechanically Informed Continuum Model of Hydrogen Embrittlement, J. Mech. Phys. Solids, 52(10), pp.2403~2430.

10.1016/j.jmps.2004.02.010

Sofronis, P., Liang, Y., Aravas, N. (2001) Hydrogen Induced Shear Localization of the Plastic Flow in Metals and Alloys, Eur. J. Mech. A Solids, 20(6), pp857~872.

10.1016/S0997-7538(01)01179-2

Sofronis, P., McMeeking, R.M. (1989) Numerical Analysis of Hydrogen Transport Near a Blunting Crack Tip, J. Mech. Phys. Solids, 37(3), pp.317~350.

10.1016/0022-5096(89)90002-1

Tiwari, G.P., Bose, A., Chakravartty, J.K., Wadekar, S.L., Totlani, M.K., Arya, R.N., Fotedar, R.K. (2000) A Study of Internal Hydrogen Embrittlement of Steels, Mater. Sci. Eng. A., 286(2), pp.269~281.

10.1016/S0921-5093(00)00793-0

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Numerical Modeling of Hydrogen Embrittlement-induced Ductile Fracture Using a Gurson-Cohesive Model (GCM) and Hydrogen Diffusion

ABSTRACT

MAIN

Fig. 1.

Schematics of the ductile fracture process in GCM

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

Fig. 2.

Algorithm of hydrogen embrittlement-induced fracture analysis

Fig. 3.

Geometry of compact tension test

Fig. 4.

Finite mesh for compact tension test

Table 1.

Material properties for parametric study

Fig. 5.

Finite mesh for compact tension test

Fig. 6.

Results of reducing only fracture energy: (a) Load-COD curves and (b) da-CTOD curves

Table 2.

Results summary of reducing only fracture energy

Fig. 7.

Results of reducing fracture energy and critical porosity: (a) Load-COD curves and (b) da-CTOD curves

Table 3.

Results summary of reducing fracture energy and critical porosity

Acknowledgements

References