Development of a Reduced Order Model using a Deep Learning-based Manifold-Augmented Approach

Seongwoo Cheon; Hyejin Kim; Seokhee Ryu; Haeseong Cho; Hakjin Lee

doi:10.7734/COSEIK.2024.37.5.337

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 October 2024. 337-344
https://doi.org/10.7734/COSEIK.2024.37.5.337

Development of a Reduced Order Model using a Deep Learning-based Manifold-Augmented Approach

매니폴드 데이터 증강기법 기반의 딥러닝 방법론을 적용한 축소 모델 개발

Seongwoo Cheon¹

Hyejin Kim²

Seokhee Ryu³⁴

Haeseong Cho⁵^*

Hakjin Lee⁶

천 성우¹

김 혜진²

류 석희³⁴

조 해성⁵^*

이 학진⁶

¹Graduate Student, Department of Aeropsace Engineering, Jeonbuk National University, Jeonju, 54896, Korea

²Graduate Student, Department of Aeropsace Engineering, Jeonbuk National University, Jeonju, 54896, Korea

³Researcher, Department of Mechanical Aerospace Engineering, Gyeongsang National University, Jinju, 52828, Korea

⁴Researcher, Quality Planning Team, Defense Agency of Technology and Quality, Jinju, 52851, Korea

⁵Asosociate Professor, Department of Aeropsace Engineering, Jeonbuk National University, Jeonju, 54896, Korea

⁶Associate Professor, Department of Mechanical Aerospace Engineering, Gyeongsang National University, Jinju, 52828, Korea

¹전북대학교 항공우주공학과 박사과정

²전북대학교 항공우주공학과 석박사통합과정

³경상국립대학교 기계항공공학부 연구원

⁴국방기술품질원 품질기획실 연구원

⁵전북대학교 항공우주공학과 부교수

⁶경상국립대학교 기계항공공학부 부교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

This study presents a deep learning-based framework to predict the aerodynamic performance of low Reynolds number airfoils. The framework employs a convolutional neural network (CNN) combined with a variational autoencoder (VAE) to efficiently handle large datasets. Moreover, the signed distance function is used as the network input to represent the airfoil configuration in the image data and parameterize the CNN. A novel generative model based on projection-based manifold learning is proposed to overcome the data mining limitation of computational fluid dynamics which may incur significant computational costs. The interpolation and extrapolation accuracy of the proposed framework is evaluated using the NACA 4-digit airfoil configuration.The results show improved accuracy via data augmentation performed by the proposed generative model.

Keywords

manifold learning

model-order reduction

deep learning

data augmentation

본 논문에서는 저 레이놀즈 수 영역에서 에어포일의 공기역학적 성능을 예측하기 위한 딥러닝 기반의 축소 모델을 제시하였다. 딥러닝 기반 축소 모델에서 CFD 해석 결과의 높은 차원의 데이터를 효율적으로 다루기 위해 변이형 오토인코더를 결합한 합성곱 신경망을 적용하였다. 부호화 거리 함수를 통해 에어포일의 형상과 유동 조건을 이미지 데이터화 하고, 이에 대해 합성곱 신경망을 매개변수화 하였다. 또한, 전산유체역학 해석의 계산 비용으로 인한 부족한 훈련 데이터를 극복하기 위해 투영 기반의 비선형 매니폴드 데이터 증강기법을 개발하였다. NACA 4계열 에어포일은 해석 예제로 고려하여 제안하는 프레임워크의 내삽과 외삽 정확도를 평가하였으며 매니폴드 데이터 증강기법을 적용하여 프레임워크의 정확도 향상을 확인하였다.

키워드

매니폴드 러닝

모델 차수 축소

딥러닝

연산유체역학

데이터 증강

MAIN

1. 서 론
2. 본 론
2.1 문제 정의
2.2 딥러닝 기반 축소 모델
2.3 매니폴드 데이터 증강기법
2.4 데이터 증강기법을 적용한 축소 모델
2.4. 수치 해석 결과
3. 결 론

1. 서 론

전산유체역학(CFD) 해석은 다양한 분야의 공학 문제를 해결하기 위해 적용되고 있으며, 이는 공간과 시간을 매우 작게 이산화하여 유체의 물리량을 높은 정확성과 신뢰성을 가지고 예측한다(Spalart and Venkatakrishnan, 2016; Xia and Sun, 2002). 하지만 전산유체역학 해석은 많은 컴퓨터 자원과 계산 시간을 요구하며 계산 비용의 절감하고자 차수 축소모델과 딥러닝 기반의 해석 방법 등의 많은 연구가 활발히 수행되었다(Balla et al., 2021).

그중에서 딥러닝 기반의 방법론은 CFD의 수학적 모델링을 블랙박스로 고려하고 해석 형상 또는 조건을 입력함에 따라 유동장의 물리량을 예측한다. Bhatnagar 등(2019)은 합성곱 오토인코더(convolutional autoencoder, CAE)를 이용한 에어포일의 속도장과 압력장 예측할 수 있는 네트워크 프레임워크를 제시하였다. 네트워크의 입력으로 signed distance function(SDF) 이미지, 받음각, 그리고 레이놀즈 수를 사용하였으며 CFD 해석 결과를 출력으로 사용하였다. Jia 등(2022)는 동적모드분해와 적합 직교 분해-장단기 메모리 네트워크을 결합한 프레임워크를 제안하고 비정상 유동의 공력 성능을 예측하였다. Lee 등(2021)은 유동의 천이 응답을 보간할 수 있는 데이터 기반의 모델 차수 축소 기법을 제시하였다. 이는 생성형 네트워크와 차원 축소 모델이 결합된 형태로 생성형 네트워크를 사용하여 에어포일 유동장의 적합 직교 계수를 예측하였다.

이러한 딥러닝 네트워크가 충분한 예측 정확성을 가지기 위해선 설계 공간을 대표하며 충분한 훈련 데이터를 구축해야 한다. 하지만, CFD 해석을 통해 충분한 훈련 데이터를 구성하는 것은 엄청난 계산 비용을 요구하며 품질이 낮은 훈련 데이터는 네트워크의 과소적합(underfitting)과 과대적합(overfitting) 등을 야기하며, 이로 인해 네트워크의 예측 정확성을 감소시킬 수 있다. 훈련 데이터의 부족을 극복하기 위해 딥러닝 네트워크 기반의 데이터 증강기법이 제시되었다(Chadebec and Allassonnière, 2022; Mumuni and Mumuni, 2022). 대표적으로 생산적 적대 신경망(generative adversarial networks, GAN)이 다양한 네트워크 문제에 대해서 데이터 증강을 위해 적용되었다. GAN은 기존의 훈련 데이터를 기준으로 추가적인 훈련 데이터를 생성한다. 하지만, GAN은 신뢰성 있는 훈련 데이터를 생성하기 위해 많은 양의 훈련 데이터를 요구한다(Salimans et al., 2016). 따라서 CFD 해석 데이터와 같이 제한된 데이터를 이용하여 훈련 데이터를 증강하기 위해 매니폴드로 정의된 설계 공간 내에서 훈련 데이터를 생성하는 매니폴드 데이터 증강기법을 고려할 수 있다(Chadebec and Allassonnière, 2021).

따라서, 본 논문에서는 CFD 해석을 통해 대규모 네트워크 훈련 데이터를 증강할 수 있는 매니폴드 기반의 접근법을 제시한다. 이를 위해 설계 공간을 축소할 수 있는 네트워크와 Geelen 등(2023)이 제시한 기법을 기반으로 적합 직교 분해의 모드를 이용하여 매니폴드를 정의하였다. 또한, 에어포일 형상에 대해 매개변수화를 수행하며 네트워크 입력과 출력을 효울적으로 구성하기 위해 합성곱 신경망과 축소모델을 결합한 프레임워크를 제시한다. 이때 딥러닝 기반의 축소모델로 적용 가능한 변이형 오토인코더(variational autoencoder, VAE)를 사용하였다. 이를 통해 에어포일 표면의 압력 분포를 예측할 수 있는 프레임워크를 설계하였으며 훈련 데이터 증강에 따른 설계 공간 내외에서의 네트워크의 예측 정확도를 확인하였다.

2. 본 론

2.1 문제 정의

본 논문에서 제안하는 딥러닝 기반의 축소모델의 목표는 다양한 매개변수에 대해서 저 레이놀즈 수 영역의 에어포일 공력 성능을 예측하는 것이다. 딥러닝 네트워크의 입력과 출력은 각각 매개변수를 포함하는 에어포일의 형상과 에어포일 표면에서의 압력 분포를 고려하였다. 이때, 에어포일의 형상에 대해서 매개변수를 효과적으로 포함하기 위해서 signed distance function(SDF)를 적용하였다. SDF는 공간상의 특정 지점의 좌표와 임의의 형상 위의 점에 대한 유클리드 거리 중 최단 거리를 반환하는 함수로 다음과 같다.

(1)

S D F (x) = \{\begin{cases} \begin{array}{ll} d (x, \partial Ω) & x \in Ω \end{array} \\ \begin{array}{ll} 0 & x \in \partial Ω \end{array} \\ \begin{array}{ll} - d (x, \partial Ω) & x \in Ω^{c} \end{array} \end{cases}

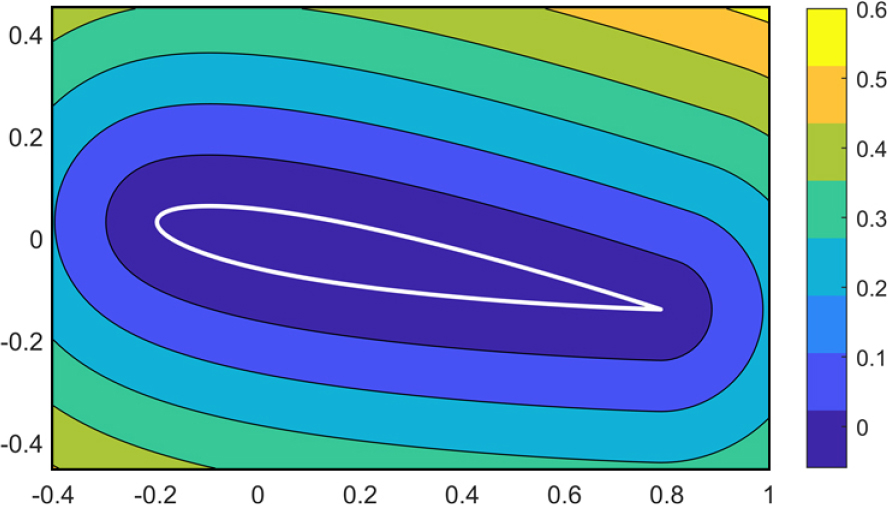
여기서, $x ∊ X$ 는 정의한 공간 내의 좌표점이고, 𝛺와 𝜕𝛺은 각각 임의의 형상과 그 경계면이다. $d (x, \partial Ω) = \min | x - x_{b} |$ 은 공간 내 좌표점과 형상 경계면의 좌표와의 가장 짧은 거리를 계산한다. 에어포일의 경계면과 멀어질수록 큰 값을 가지며 내부는 음의 값을 가진다. Fig. 1은 SDF를 통해 생성한 에어포일 이미지 데이터의 예시이다. 또한, 에어포일의 압력 데이터는 전산유체역학 해석을 통해 획득하였으며 상용 프로그램인 ANSYS Fluent를 사용하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F1.jpg

Fig. 1.

A signed distance function contour plotted for the NACA 0012 with angle of attack 10°

2.2 딥러닝 기반 축소 모델

2.2.1 변이형 오토인코더

딥러닝 기반의 네트워크를 구성하기 위한 입력과 출력의 차원 크기는 네트워크 훈련 측면에서 중요한 역할을 한다. 따라서 큰 차원을 가지는 데이터의 특징을 보존하면서 축소된 데이터 형태로 나타내는 것이 중요하다. VAE는 딥러닝 기반의 차원 축소모델을 설계하기 위해 적용할 수 있다.

VAE는 비지도 학습 네트워크 중 하나로 인코더 $q_{ϕ} (z | x; ϕ)$ 와 디코더 $q_{θ} (z | x; θ)$ 로 구성된 대칭형 구조와 잠재 공간으로 축소된 데이터가 임의의 확률 분포를 가지게 하는 변이형 연산자를 사용한다. 따라서, 인코더 $q_{ϕ} (z | x; ϕ)$ 는 입력되는 데이터를 식 (1)에 따라서 평균 𝜇과 편차 𝜎를 가지는 분포로 축소된 잠재 공간으로 표현한다. 디코더 $q_{θ} (z | x; θ)$ 는 식 (2)와 같이 잠재 공간에서 임의의 데이터를 샘플링하고 식 (3)을 통해 원래의 차원으로 복원한다.

(1)

q_{ϕ} (z | x; ϕ) = N (z; μ (x), σ (x)^{2})

(2)

z = μ + σ ⊙ ϵ, ϵ ~ N (0, 1)

(3)

\hat{x} = q_{θ} (x | z; θ)

2.2.2 합성곱 신경망

합성곱 신경망은 합성곱 계층과 완전 연결 계층으로 구성된 딥러닝 네트워크로 입력 이미지에 대해 분류 모델 또는 회귀 모델을 학습한다. 합성곱 필터를 이용하여 입력값과 데이터 위치 정보에 따른 특징을 학습하게 되며 합성곱 계층을 형성한다. 또한 완전 연결 계층은 출력에 대해 분류 모델 또는 회귀 모델을 학습한다. 합성곱 신경망은 가중치(weight)와 편향(bias)을 최적화하여 네트워크를 구축하며 식 (4)와 같다.

(4)

y_{u, v}^{(n)} = f^{(n)} (b_{u, v} + \sum_{i = - k_{h}}^{k_{h}} \sum_{j = - k_{w}}^{k_{w}} w_{i, j}^{(n)} x_{u - i, v - j}^{(n - 1)})

이때, $x_{u - i, v - j}^{(n - 1)}$ 와 $y_{u, v}^{(n)}$ 는 각각 $(n - 1)$ 번째 합성곱 계층과 합성곱 필터로부터 계산되는 출력이다. $w_{i, j}^{(n)}$ 와 $b_{u, v}$ 은 $n$ 번째 합성곱 필터의 가중치와 편향이다.

딥러닝 네트워크의 매개변수화는 훈련된 네트워크의 효율적인 사용과 설계 공간에서 임의 입력의 정확한 예측을 위해 필요하다. 따라서 합성곱 신경망의 입력 및 출력은 설계 공간을 구성하는 변수를 고려하여 설정해야 하며, 본 논문에서는 CFD 해석 조건과 결과를 반영하기 위해 SDF 결과와 적합 직교 분해를 통해 축소된 데이터를 각각 합성곱 신경망의 입력과 출력으로 고려하였다.

2.3 매니폴드 데이터 증강기법

2.3.1 적합 직교 분해

적합 직교 분해는 완전 차수 데이터를 나타낼 수 있는 직교 기저를 제시하며 데이터 세트의 정보 손실을 최소화할 수 있는 축소 기저를 구축하여 데이터를 저차원 공간으로 투영한다. 따라서, 데이터 기반의 매니폴드의 기저 벡터를 정의하기 위해 적용될 수 있다. 특이값 분해를 통한 적합 직교 분해는 식 (5)와 같다.

(5)

U = Φ Σ V^{T}

여기서, $Φ ∊ ℝ^{N_{h} \times N_{h}}$ 와 $V ∊ ℝ^{N_{s} \times N_{s}}$ 는 직교 벡터 집합이며, $Φ = \{ϕ_{1}, ϕ_{2}, \dots, ϕ_{N_{h}}\}$ 은 적합 직교 벡터로 구성된다. $Σ = \{σ_{1}, σ_{2}, \dots, σ_{N_{h}}\}$ 는 특이값을 포함하는 대각 행렬이다. $U ∊ ℝ^{N_{h} \times N_{s}}$ 은 매니폴드를 구성하는 데이터의 스냅샷 행렬이며, $N_{h}$ 와 $N_{s}$ 은 수집된 벡터의 크기와 개수이다. 시스템을 대표할 수 있는 $r$ 개 만큼의 기저 벡터 $Φ_{r} = {ϕ_{1}, ϕ_{2}, \dots, ϕ_{r}}$ 를 선택하여 식 (6)과 같이 스냅샷을 축소한다.

(6a)

U = \sum_{i = 1}^{N_{h}} α_{i} ϕ_{i} \approx \sum_{i = 1}^{r} α_{i} ϕ_{i}

(6b)

α = Φ_{r} U'

2.3.2 데이터 기반 2차 비선형 매니폴드

본 논문에서 설계 공간을 근사하기 위해 Geelen 등(2023)이 제시한 매니폴드 기법을 적용하였다. 이는 해석 데이터로부터 차수 감소 모델 연산자를 추론하는 연산자 추론 방법을 기반으로 한다. 해석을 통해 얻은 데이터를 적합 직교 분해를 이용하여 기저 벡터를 도출하고 선형과 비선형 공간으로 근사한다. 이때, 2차 비선형 매니폴드는 식 (7)과 같이 정의할 수 있다.

(7)

S \approx S_{p r o j} = S_{r e f} + V \hat{S} + \bar{V} (\hat{S} \otimes \hat{S})

$S$ 는 해석 결과로 구성된 행렬이며 $S_{r e f}$ 는 $S$ 의 평균값이다. $V$ 는 스냅샷 행렬의 적합 직교 분해를 통해 도출된 기저 벡터 이다. $\hat{S}$ 은 스냅샷의 축소 데이터로 식 (6b)으로 계산된다. $\bar{V}$ 는 매니폴드의 비선형 항을 계산하는 연산자이다. 이는 선형 조합으로 근사되는 적합 직교 분해의 오차가 최소화되도록 계산되며 식 (8)과 같이 최소자승법문제로 고려할 수 있다. 또한, 매니폴드의 근사 오차는 식 (9)를 통해 계산할 수 있다.

(8a)

\bar{V} = \arg \sum_{j = 1}^{k} {‖ s_{j} - s_{r e f} - \hat{V s_{j}} - \bar{V} ({\hat{s}}_{r e f} \otimes {\hat{s}}_{r e f}) ‖}_{2}^{2}

(8b)

\bar{V} = (I - V V^{T}) (S - S_{r e f}) W^{T} (W W^{T})^{- 1}

(9)

e = ∥ S - S_{p r o j} ∥_{F}^{2} / ∥ S ∥_{F}^{2}

본 논문에서는 설계 공간을 효과적으로 나타내기 위해 비지도학습 네트워크인 CAE를 적용하였다. 따라서, 설계 변수로 고려한 에어포일의 형상과 압력 분포를 CAE에 입력하여 잠재 공간으로 데이터를 표현하였다. 이후 잠재 벡터와 이에 대응하는 설계 변수를 이용하여 비선형 매니폴드로 정의하고 설계 공간 위의 데이터를 추출하기 위해 Latin hypercube sampling (LHS) 기법을 적용하여 설계 공간을 대표하는 데이터를 생성하였다. 이후, CAE의 디코더를 이용하여 원래의 차원으로 복원하며 이는 에어포일의 형상과 압력 계수이다.

2.4 데이터 증강기법을 적용한 축소 모델

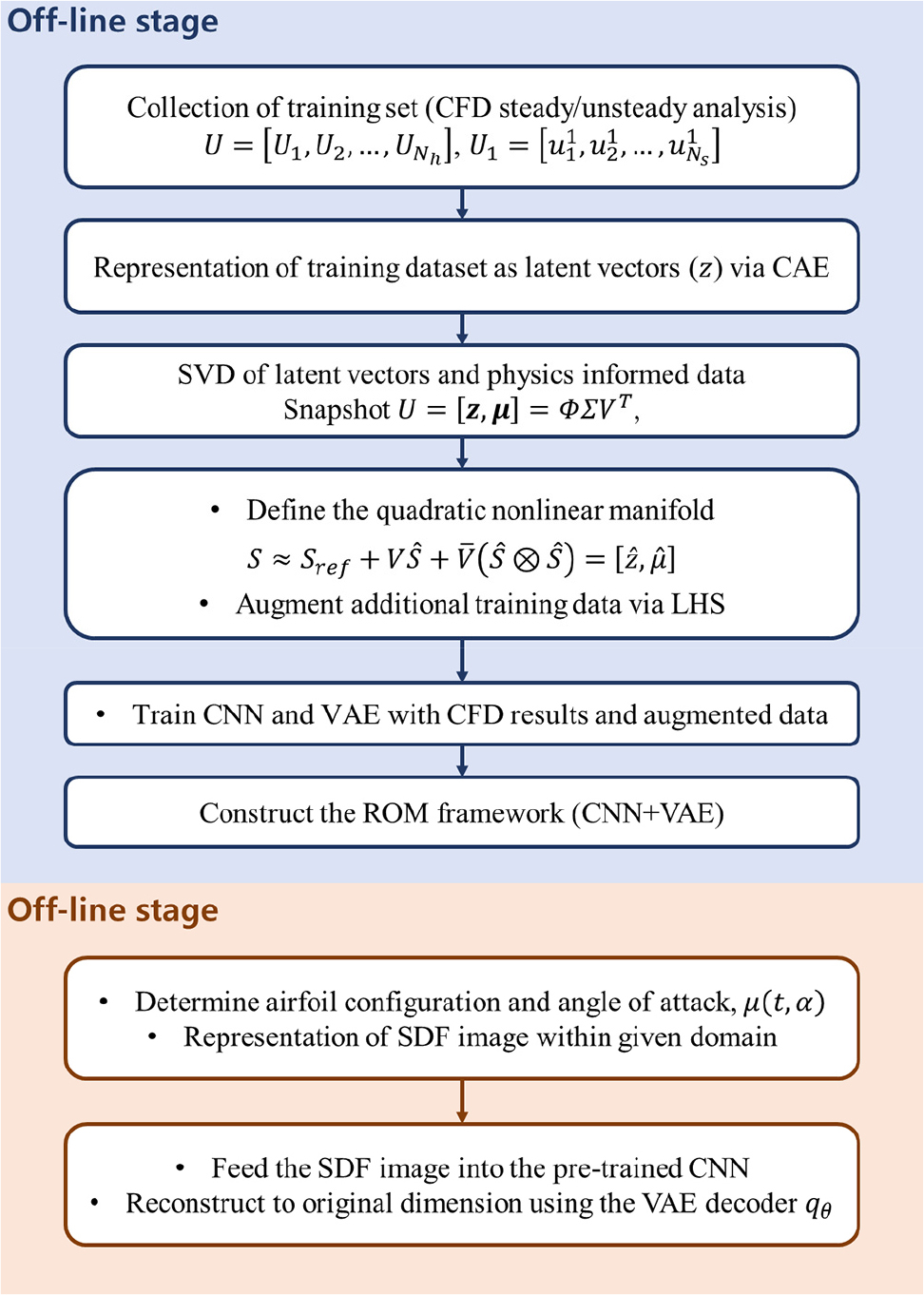
본 논문에서 제시하는 데이터 증강기법을 적용한 축소모델의 절차는 Fig. 2와 같으며, 전반적인 과정은 off-line 및 on-line 단계로 구성된다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F2.jpg

Fig. 2.

Outline of proposed frameworks

Off-line 단계에서는 CFD 해석을 수행하여 데이터 세트를 구성하고 딥러닝 기반 축소모델을 구축하는 것이다. 이때 훈련 데이터를 구성하기 위해 매니폴드 데이터 증강기법이 적용하였다. 먼저, 비선형 매니폴드를 정의하기 위한 잠재 벡터를 추출하기 위해 에어포일의 압력 분포와 데카르트 좌표를 포함한 입력 데이터를 구성하고 CAE를 이용하여 잠재 벡터로 표현한다. 잠재 벡터와 설계 변수를 이용하여 스냅샷 행렬을 구성하여 비선형 매니폴드를 정의하였다. LHS를 사용하여 비선형 다양체에서 $N$ 개의 데이터를 추출하고 훈련된 CAE의 디코더를 사용하여 원래의 차원으로 복원한다.

증강된 훈련 데이터와 기존 훈련 데이터를 결합하여 새로운 훈련 데이터 세트를 구성한다. 압력 계수 데이터는 적합 직교 분해를 통해 축소된 데이터로 나타내며 익형 데이터는 SDF를 통해 이미지 데이터로 변환한다. 이후, 합성곱 신경망의 입력과 출력으로 구성하여 네트워크를 훈련한다.

On-line 단계는 off-line 단계에서 구축한 프레임워크를 바탕으로 다양한 매개변수에 대한 에어포일의 압력 분포 예측을 수행하는 단계이다. 먼저, 설계 공간 내에서 에어포일의 형상과 받음각을 결정하고 SDF 이미지 데이터를 생성한다. 합성곱 신경망에 입력으로 넣어 압력 계수 분포의 축소된 데이터는 예측한다. 이후, 식 (4)를 통해 원래의 차원으로 복원된다.

2.4. 수치 해석 결과

2.4.1 해석 예제 및 CFD 해석

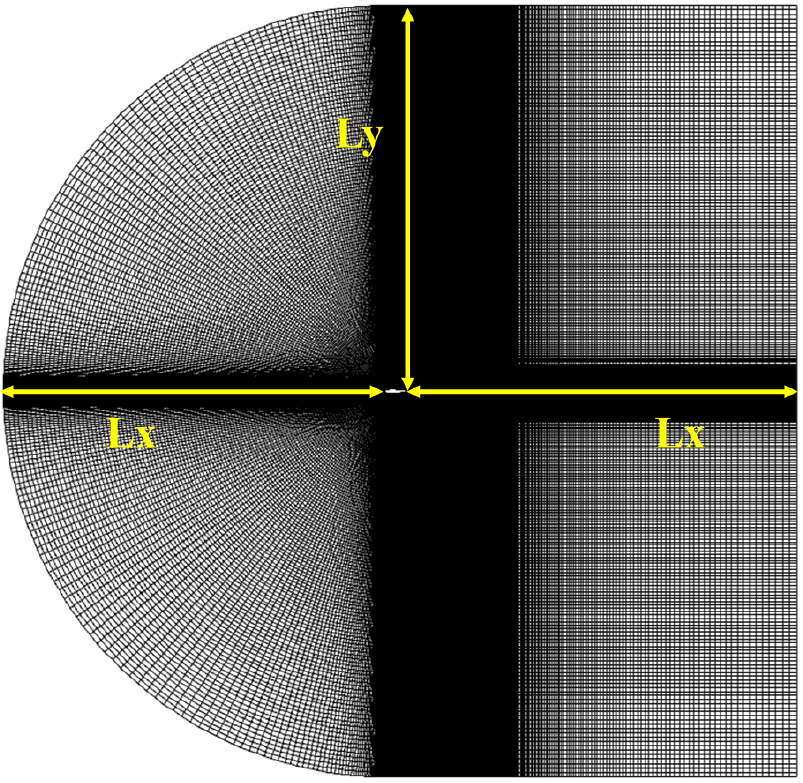
훈련 데이터 생성을 위해 고려한 해석 예제는 시위선 길이가 1이며 캠버가 없는 NACA 4계열 에어포일을 고려하였다. Fig. 2와 같이 CFD 해석 공간은 C자 형식 구조를 고려하였으며 400,000개 요소로 이산화하였다. 이때, 해석 공간의 x 방향 (Lx)과 y 방향(Ly)의 길이는 시위선의 15배로 설정하였다. 해석 조건으로 Re = 50,000과 M = 0.03을 고려하였다.

본 논문에서는 설계 공간 $μ (t, α)$ 으로 에어포일의 두께 $t$ 와 받음각 𝛼으로 설정하였다. Fig. 3은 설계 공간을 나타내며 $t ∊ [0, 24]$ , $α ∊ [0, 12]$ 이다. 훈련 데이터는 받음각을 1도씩 증가하며 에어포일은 NACA 0006, 0008, 0009, 0010, 0012, 0015, 0018, 0021, 0024을 고려하였다. 따라서, 훈련 데이터로 117개의 케이스를 선정하였다. 훈련된 딥러닝 기반 축소모델의 정확성을 평가하기 위해 내삽 문제와 외삽 문제를 고려하였으며 각각 𝜇=(22, 9)와 𝜇=(24, 7)이다. 이때 외삽은 설계 공간의 경계에 위치한 데이터이다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F3.jpg

Fig. 3.

C-grid mesh and boundary condition

2.4.2 축소 모델 예측 결과

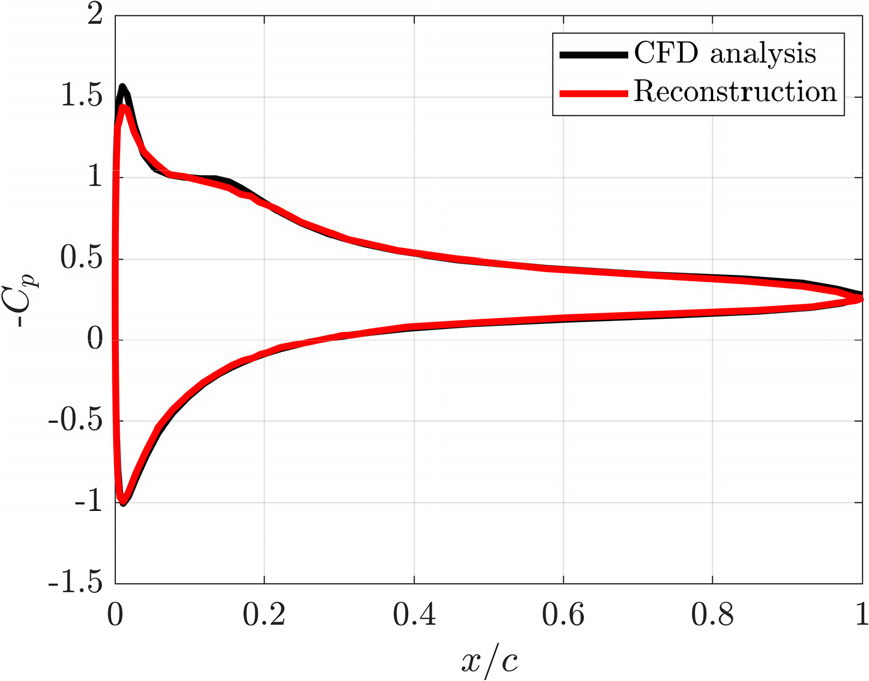
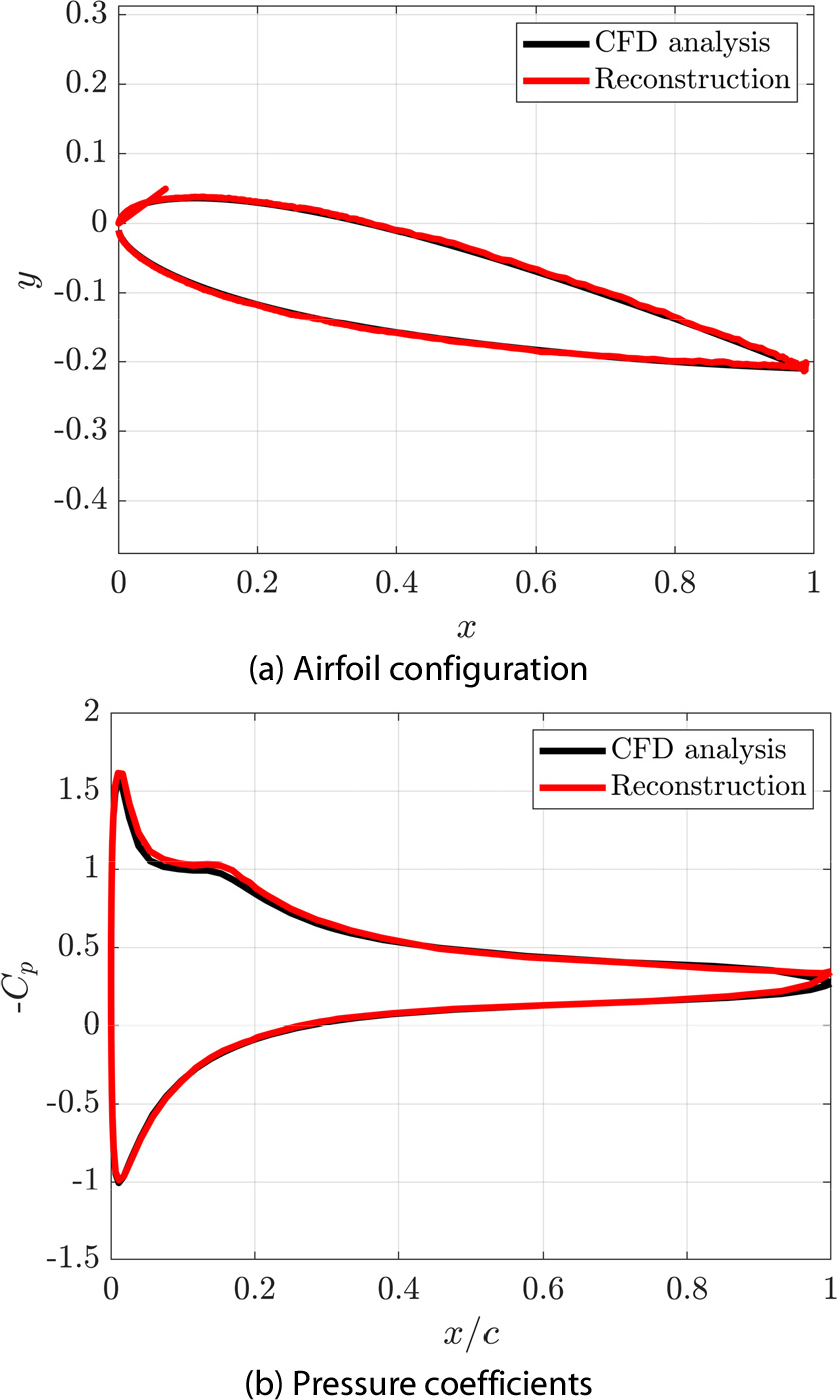
딥러닝 기반 축소모델의 정확성을 검증하기 이전에 적합 직교 모드를 이용한 축소된 데이터의 정확성을 검토하였다. CFD 해석 결과로부터 에어포일 포면 압력 분포를 획득하고 VAE의 입력 데이터의 크기는 $x ∊ ℝ^{939 \times 117}$ 이다. VAE를 통해 축소된 압력 데이터는 $z ∊ ℝ^{20 \times 117}$ 로 나타내었다. Fig. 4는 VAE를 통해 축소 및 복원된 𝜇=(10, 10)의 압력 분포이며, 훈련 데이터에 대해서 정규화한 평균 제곱근 오차(normalized root mean square error, NRMSE)가 최대 14.43%이다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F4.jpg

Fig. 4.

Reconstruction of Pressure coefficients of 𝜇=(18, 12) using VAE before data augmentation

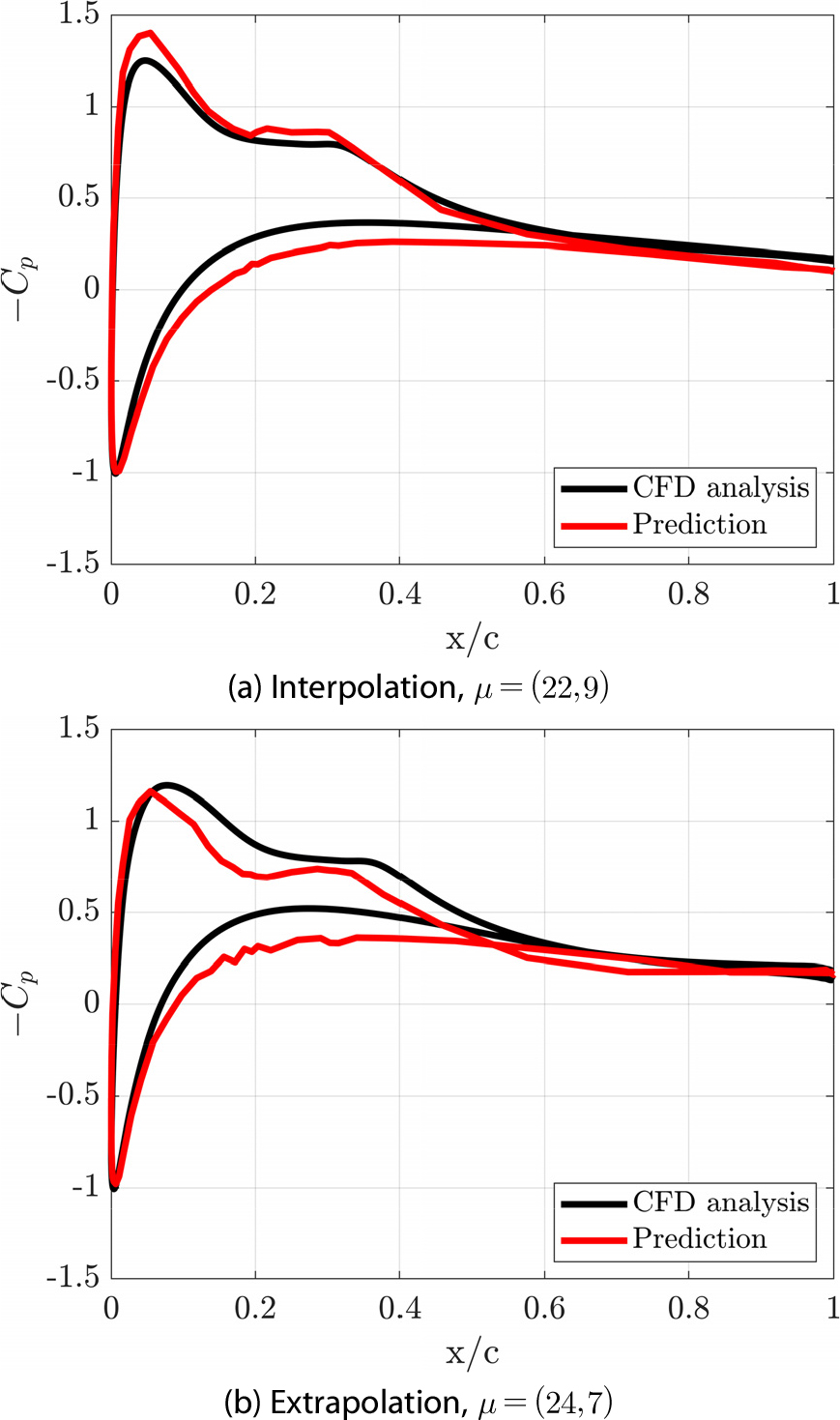
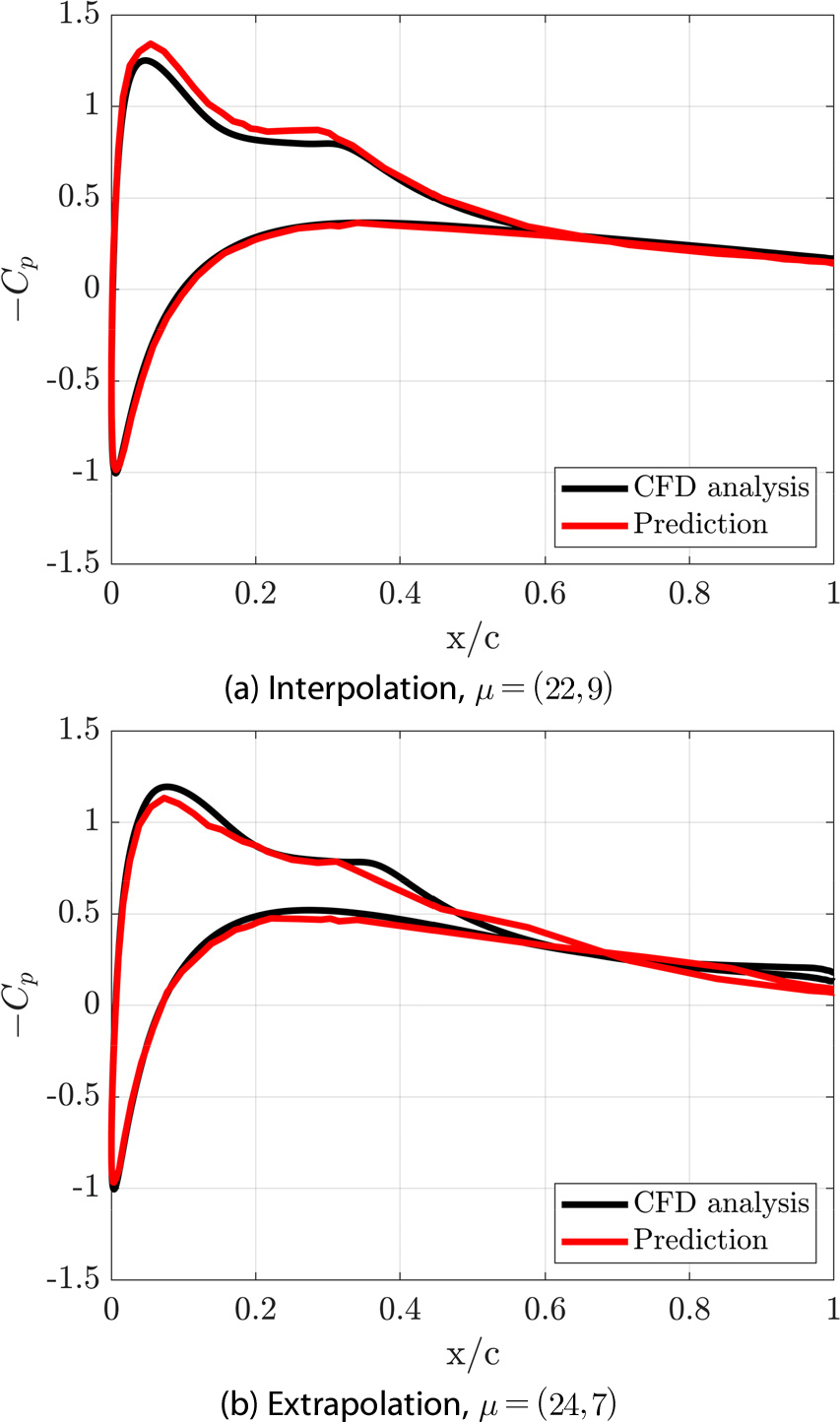
Fig. 5(a)는 설계 공간의 내삽 설계 변수 중 𝜇=(22, 9)의 압력 계수 분포를 예측한 결과이다. 압력 계수 분포의 NRMSE가 14.87%이며 결정 계수(coefficient of determination, R²)가 0.97 이상임을 확인하였다. 하지만, Fig. 5(b)에서 확인할 수 있듯 설계 공간의 외삽 𝜇=(24, 7)에 대해서 축소 모델 네트워크의 예측 성능이 감소하는 것을 확인하였다. 외삽 예측 성능에 대해서 NRMSE가 22.69%이며 R²가 0.95로 예측 정확도가 감소하였다. 내삽과 외삽에 대한 오차는 Table 1에 정리하였다.

Table 1.

Prediction accuracy of 𝜇=(22, 9) and 𝜇=(24, 7) before data augmentation

$C_{p}$	Interpolation	Extrapolation
NRMSE (%)	14.87	22.69
R2 (-)	0.97	0.95

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F5.jpg

Fig. 5.

Prediction results of pressure distribution before data augmentation

내삽 예제에 대해서 본 논문에서 제시하는 프레임워크는 NRMSE가 14.87%로 예측 성능을 보였지만 에어포일의 윗면에서 특히 오차가 크게 발생하며 외삽에 대해서는 예측이 어려움을 확인할 수 있다. 따라서, 훈련 데이터를 증강하고 축소모델의 네트워크 예측 성능을 향상시키기 위해서 설계 공간 내부와 경계 근처에서 LHS을 이용하여 매니폴드 데이터 증강기법을 적용하였다.

2.4.3 데이터 증강

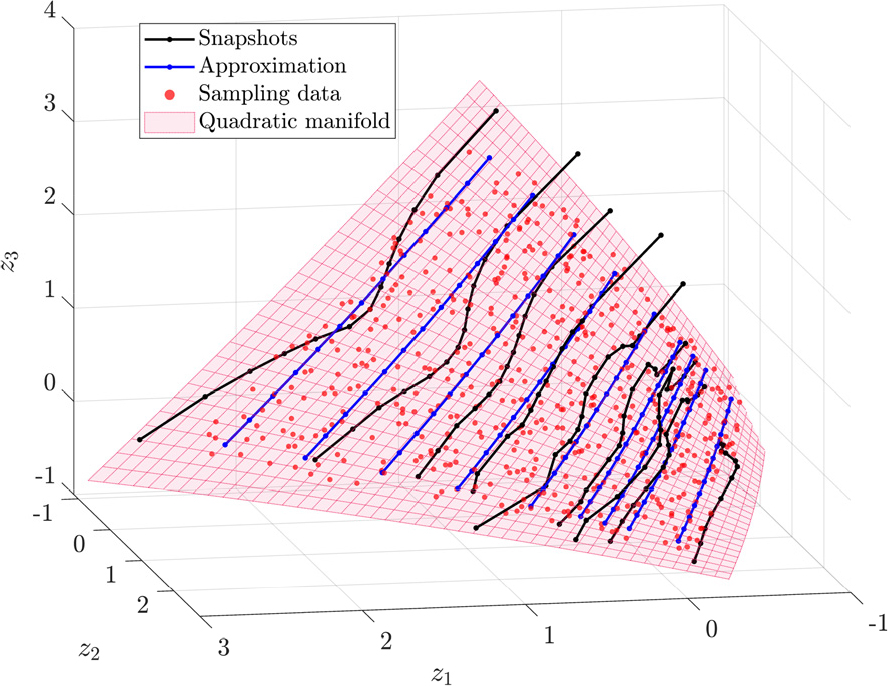
압력 계수와 에어포일 좌표를 설계 공간으로 설정하고 CAE를 통해 축소된 설계 공간을 표현하였다. 이후 축소된 데이터와 설계 변수 $t$ , 𝛼를 이용하여 스냅샷 $U ∊ ℝ^{5 \times 117}$ 을 구성하였으며 정의한 2차 비선형 매니폴드는 Fig. 6과 같다. 이때 적합 직교 분해를 통해 도출된 기저 벡터는 2개를 사용하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F6.jpg

Fig. 6.

Quadratic manifold in design space reduced by CAE

매니폴드의 근사 오차는 0.11이며 Fig. 7은 매니폴드 위의 훈련 데이터 𝜇=(18, 12)을 CAE의 디코더로 복원한 결과이다. 따라서 정의한 비선형 매니폴드는 설계 공간의 특징을 포함한다. 이후 LHS을 이용하여 500개의 훈련 데이터를 생성하였으며 생성한 데이터는 Fig. 6에 빨간 점으로 표시하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F7.jpg

Fig. 7.

Reconstruction of pressure distribution and airfoil configuration of 𝜇=(18, 12) via proposed approach

2.4.4 데이터 증강을 적용한 축소 모델 예측 결과

데이터 증강 이후, VAE에 입력되는 에어포일 표면의 압력 분포 데이터의 크기는 $x ∊ ℝ^{939 \times 617}$ 이며 축소된 데이터의 크기는 이전과 동일하다. Fig. 8는 VAE를 통해 축소 및 복원된 𝜇=(18, 12)의 압력 분포이다. NRMSE가 최대 9.91%으로 데이터 증강기법의 적용으로 VAE의 비지도 학습의 예측 성능이 향상되었다.

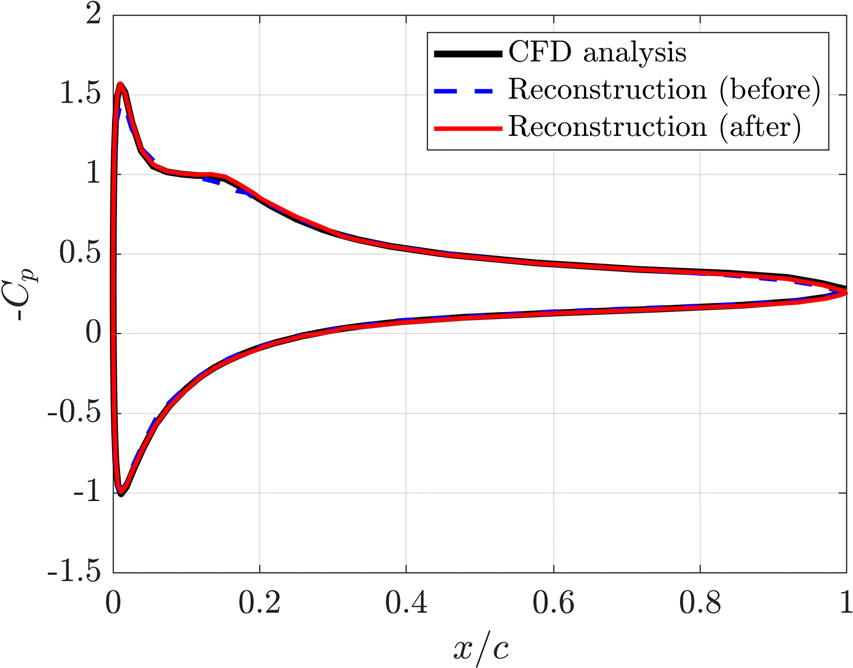
https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F8.jpg

Fig. 8.

Reconstruction of Pressure coefficients of 𝜇=(18, 12) using VAE before data augmentation

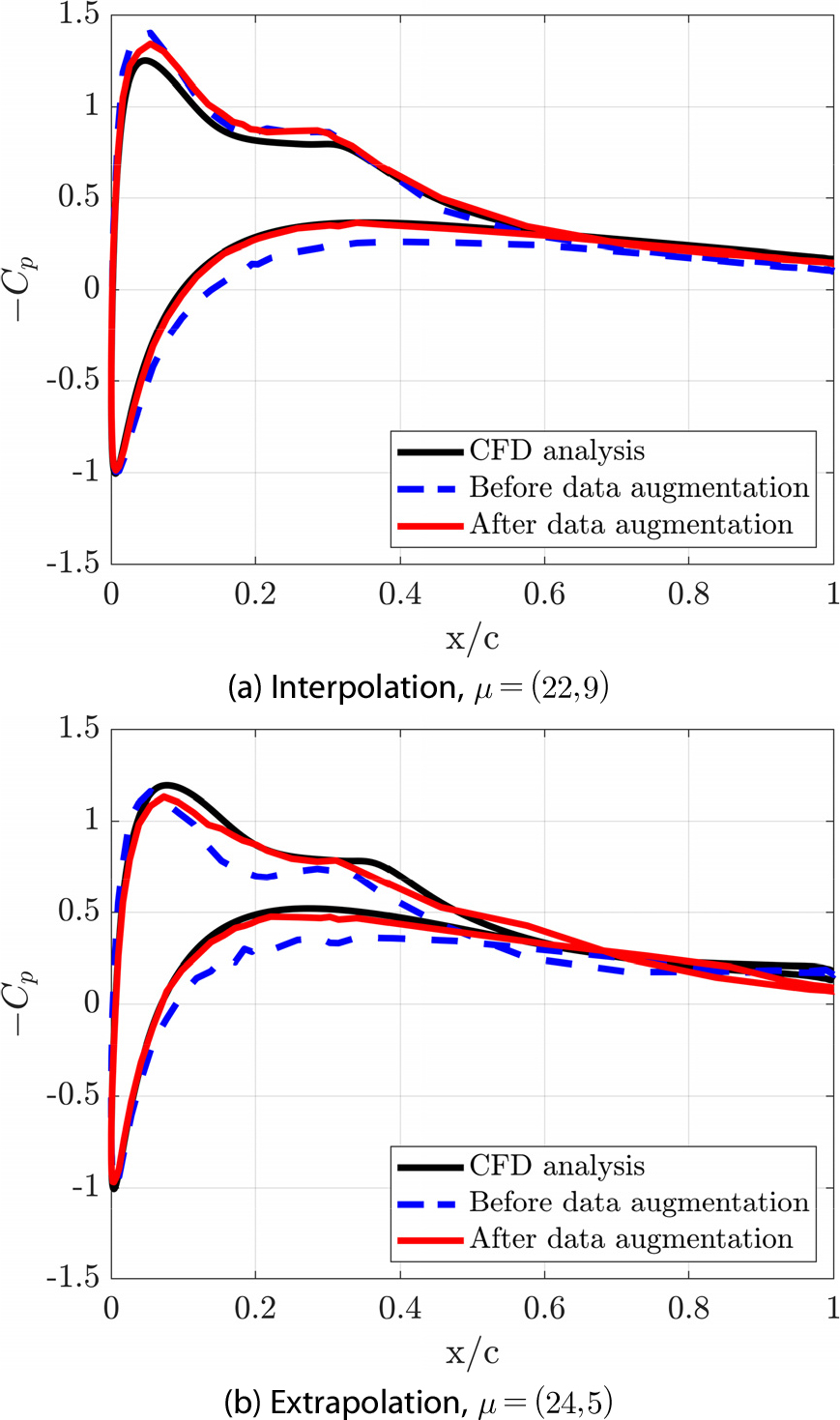
Fig. 9는 내삽 𝜇=(22, 9)과 외삽 𝜇=(24, 7)에 대한 축소 모델의 예측 결과이다. 내삽의 NRMSE와 R²는 각각 8.21%, 0.99임을 확인하였다. 또한, 외삽의 NRMSE는 11.64%, 0.99이다. 따라서 고려한 내삽과 외삽 테스트 케이스에 대해서 NRMSE가 각각 약 6.66%와 11.05% 감소하였으며 Fig. 10을 통해 축소모델의 예측 정확도가 향상되었음을 확인할 수 있다. Table 2는 데이터 증강 이후 축소모델의 예측 정확성을 나타낸다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F9.jpg

Fig. 9.

Prediction results of pressure distribution after data augmentation

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F10.jpg

Fig. 10.

Prediction results of pressure distribution before data augmentation

Table 2.

Prediction accuracy 𝜇=(22, 9) and 𝜇=(24, 7) after data augmentation

$C_{p}$	Interpolation	Extrapolation
NRMSE (%)	8.21	11.64
R2 (-)	0.99	0.99

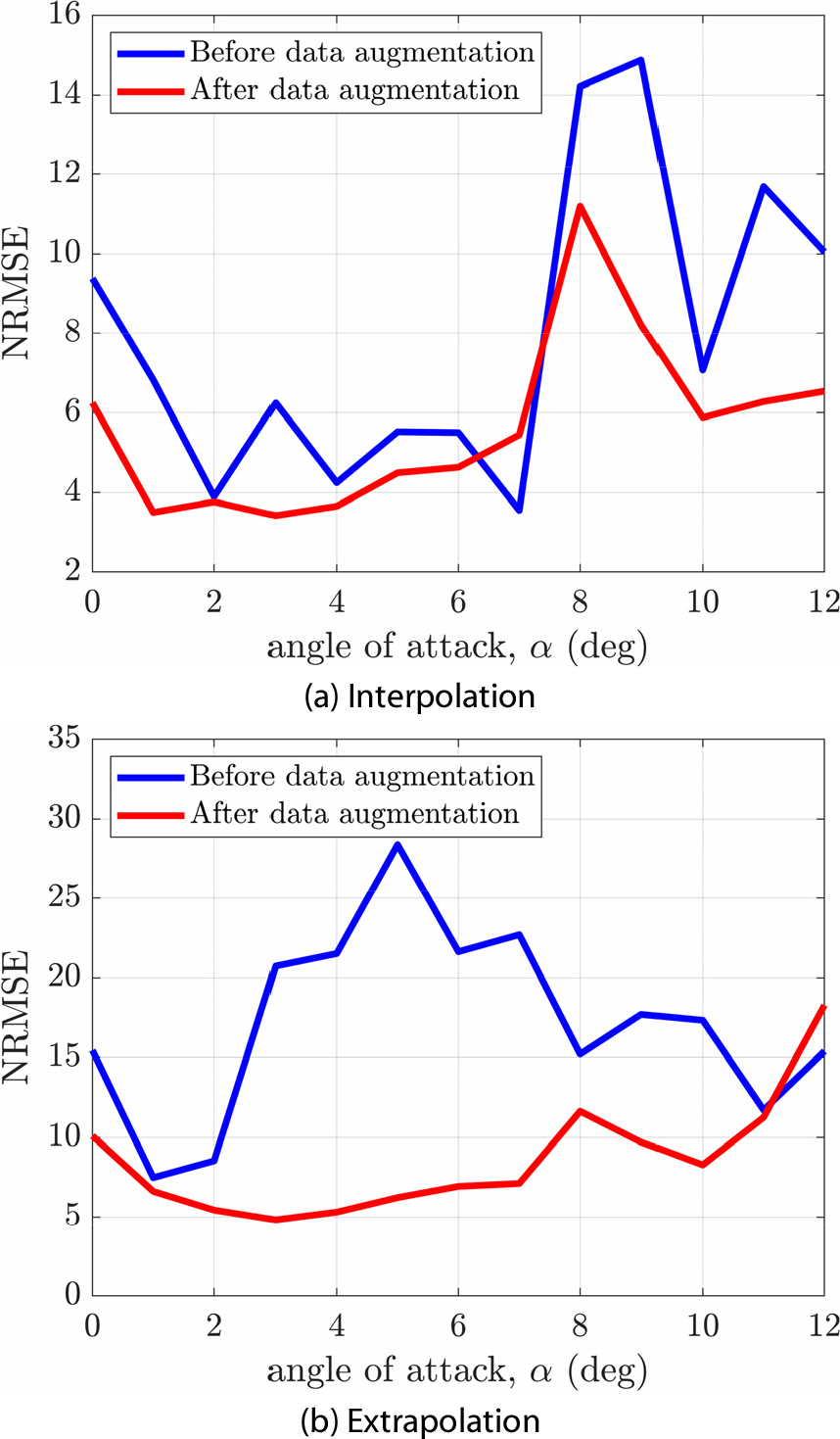
Fig. 11은 내삽 예측에 대한 𝜇=(22, 11)와 𝜇=(24,5)이외에 다른 받음각에서 내삽과 외삽에 대한 데이터 증강 전후의 축소모델의 NRMSE를 나타낸다. 내삽의 경우 고려한 전체 받음각 구간에서 NRMSE가 감소하거나 유사한 값을 보이며 외삽의 경우 전체 받음각 구간에서 NRMSE가 감소하였다. 하지만, Fig. 10(b)을 확인하였을 때 여전히 높은 오차를 확인하였다. 따라서, 본 논문에서 제시하는 매니폴드 기반의 데이터 증강기법은 딥러닝 기반 축소모델의 내삽 성능을 향상시킬 수 있지만 외부 설계 공간의 특징을 정확하게 포함하지 않아 외삽 성능 예측에는 제한적인 성능 향상을 확인하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370506/images/Figure_jcoseik_37_05_06_F11.jpg

Fig. 11.

NRMSEs of interpolation and extrapolation according to angle of attack after data augmentation

3. 결 론

본 논문에서는 합성곱 신경망과 VAE를 결합하여 딥러닝 기반의 차원 축소모델을 제시하고 저 레이놀즈 수 영역에서 에어포일의 공력 성능 예측하였다. 이 때 에어포일의 형상과 받음각을 표현하기 위해 SDF를 통해 이미지로 데이터로 변환하였으며 압력 계수 분포는 VAE를 축소된 데이터로 표현하였다. 또한, CFD 해석의 계산 비용으로 인한 충분한 훈련 데이터 생성의 제한점을 개선하기 위해 매니폴드 기반의 데이터 증강기법을 개발하였다. 이 기법은 고차원의 설계 공간을 CAE를 통해 촉소된 설계 공간으로 표현하고 잠재 벡터와 설계 변수를 이용하여 설계 공간을 투영 기반의 2차 비선형 매니폴드로 정의한다.

제시한 딥러닝 기반의 축소모델과 매니폴드 데이터 증강기법의 성능을 검증하기 위해 저 레이놀즈 수 영역에서 캠버가 없는 NACA 4계열 에어포일을 고려하였다. 설계 공간의 내삽 및 외삽 데이터를 검증 데이터로 활용하였다. 데이터 증강에 따라 내삽과 외삽의 예측 성능은 NRMSE를 기준으로 각각 약 6.66%, 10.05%의 예측 정확도가 향상되었으며 결과적으로 𝜇=(22,11)와 𝜇=(24,5)에 대해서 각각 8.21%, 11.64%의 정확도로 예측하였다.

Acknowledgements

본 연구는 2022년 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원(No.2022M1A3C2076483)을 받아 수행되었습니다.

References

Balla, K., Sevilla, R., Hassan, O., Morgan, K. (2021) An Application of Neural Networks to the Prediction of Aerodynamic Coefficients of Aerofoils and Wings, Appl. Math. Model., 96, pp.456~479.

10.1016/j.apm.2021.03.019

Bhatnagar, S., Afshar, Y., Pan, S., Duraisamy K., Kaushik, S. (2019) Prediction of Aerodynamic Flow Fields using Convolutional Neural Networks, Comput. Mech., 64, pp.525~545.

10.1007/s00466-019-01740-0

Chadebec, C., Allassonnière, S. (2021) Data Augmentation with Variational Autoencoders and Manifold Sampling, In Deep Generative Models, and Data Augmentation, Labelling, and Imperfections: First Workshop, DGM4MICCAI 2021, and First Workshop, DALI 2021, Held in Conjunction with MICCAI 2021, Proceedings 1, pp.184~192.

10.1007/978-3-030-88210-5_17

Chadebec, C., Allassonnière, S. (2022) A Geometric Perspective on Variational Autoencoders, Adv. Neural Inf. Proc. Syst., 35, pp.19618~19630.

Geelen, R., Wright, S., Willcox, K. (2023) Operator Inference for Non-Intrusive Model Reduction with Quadratic Manifolds, Comput. Methods App. Mech. & Eng., 403, p.115717.

10.1016/j.cma.2022.115717

Jia, X., Li, C., Ji, W., Gong, C. (2022) A Hybrid Reduced-Order Model Combing Deep Learning for Unsteady Flow, Phys. Fluids, 34(9), p.097112.

10.1063/5.0104848

Lee, S., Jang, K., Cho, H., Kim, H., Shin, S. (2021) Parametric Non-Intrusive Model order Reduction for Flow-Fields using Unsupervised Machine Learning, Comput. Methods Appl. Mech. & Eng., 384, p.113999.

10.1016/j.cma.2021.113999

Mumuni, A., Mumuni, F. (2022) Data Augmentation: A Comprehensive Survey of Modern Approaches, Array, 16, p.100258.

10.1016/j.array.2022.100258

Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V., Radford, A., Chen, X. (2016) Improved Techniques for Training GANs, Adv. Neural Inf. Proc. Syst., 29.

Spalart, P.R., Venkatakrishnan, V. (2016) On the Role and Challenges of CFD in the Aerospace Industry, The Aeronaut. J., 120(1223), pp.209~232.

10.1017/aer.2015.10

Xia, B., Sun, D.-W. (2002) Applications of Computational Fluid Dynamics (CFD) in the Food Industry: A Review, Comput. & Electron. Agric., 34(1-3), pp.5~24.

10.1016/S0168-1699(01)00177-6

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Development of a Reduced Order Model using a Deep Learning-based Manifold-Augmented Approach

ABSTRACT

MAIN

(1)

Fig. 1.

A signed distance function contour plotted for the NACA 0012 with angle of attack 10°

(1)

(2)

(3)

(4)

(5)

(6a)

(6b)

(7)

(8a)

(8b)

(9)

Fig. 2.

Outline of proposed frameworks

Fig. 3.

C-grid mesh and boundary condition

Fig. 4.

Reconstruction of Pressure coefficients of 𝜇=(18, 12) using VAE before data augmentation

Table 1.

Prediction accuracy of 𝜇=(22, 9) and 𝜇=(24, 7) before data augmentation

Fig. 5.

Prediction results of pressure distribution before data augmentation

Fig. 6.

Quadratic manifold in design space reduced by CAE

Fig. 7.

Reconstruction of pressure distribution and airfoil configuration of 𝜇=(18, 12) via proposed approach

Fig. 8.

Reconstruction of Pressure coefficients of 𝜇=(18, 12) using VAE before data augmentation

Fig. 9.

Prediction results of pressure distribution after data augmentation

Fig. 10.

Prediction results of pressure distribution before data augmentation

Table 2.

Prediction accuracy 𝜇=(22, 9) and 𝜇=(24, 7) after data augmentation

Fig. 11.

NRMSEs of interpolation and extrapolation according to angle of attack after data augmentation

Acknowledgements

References