Prediction of the Mechanical behavior of Short-Fiber Reinforced Composite Structures using Compression Molding-Structural Coupled Analysis

Da-Young Jang; Geung-Hyeon Lee; Jang-Woo Han

doi:10.7734/COSEIK.2024.37.5.317

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 October 2024. 317-326
https://doi.org/10.7734/COSEIK.2024.37.5.317

Prediction of the Mechanical behavior of Short-Fiber Reinforced Composite Structures using Compression Molding-Structural Coupled Analysis

압축 성형-구조 연계 해석을 활용한 단섬유 강화 복합소재 구조물의 기계적 거동 예측

Da-Young Jang¹^*

Geung-Hyeon Lee¹

Jang-Woo Han²

장 다영¹^*

이 긍현¹

한 장우²

¹Graduate Student, Department of Mechanical Engineering, Kumoh National Institute of Technology, Gumi, 39177, Korea

²Assistant Professor, School of Mechanical System Engineering, Kumoh National Institute of Technology, Gumi, 39177, Korea

¹국립금오공과대학교 기계공학과 석사과정

²국립금오공과대학교 기계시스템공학부 조교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In this paper, compression molding-structural coupled analysis was proposed to accurately consider the effect of initial compression molding conditions on the mechanical behavior of short-fiber reinforced composite structures. To this end, local short-fiber orientations depending on the initial charge conditions were investigated using compression molding analysis, and a mean-field homogenization scheme was employed to efficiently derive equivalent orthotropic material properties determined by short-fiber orientations. Furthermore, based on the refined finite element model with short-fiber orientation, compression molding-structural coupled analysis precisely described the locally independent mechanical behavior induced by initial molding conditions. Consequently, it could be confirmed that the proposed analysis model provides a reasonable solution in the design process of short-fiber reinforced composite structures manufactured by compression molding.

Keywords

composite structures

compression molding-structural coupled analysis

short-fiber orientation

orthotropic material property

본 논문에서는 초기 압축 성형 공정 조건들이 단섬유 강화 복합소재 구조물의 기계적 거동 특성에 미치는 영향을 효과적으로 반영할 수 있는 압축 성형-구조 연계 해석 방안을 제안하였다. 압축 성형 해석을 바탕으로 초기 charge의 형상 및 배치에 따른 부위별 단섬유 배향 특성을 분석하였으며, 평균장 균질화 이론을 통해 단섬유 배향 특성에 따른 등가 이방 물성을 도출하였다. 나아가, 단섬유 배향 정보가 Mapping된 유한요소 모델을 기반으로 초기 공정 조건들에 의해 야기되는 부위별 거동 특성 변화를 고려할 수 있는 압축 성형-구조 연계 해석을 진행하였다. 관련 수치 예제 검증을 통해 제시된 해석 방안은 압축 성형을 통해 제작된 단섬유 강화 복합소재 구조물 설계 과정에서 효과적인 솔루션을 제공함을 확인하였다.

키워드

복합소재 구조물

압축 성형-구조 연계해석

단섬유 배향

이방 물성

MAIN

1. 서 론
2. 단섬유 강화 복합소재 구조물에 대한 압축 성형 해석
2.1 압축 성형 해석을 위한 초기 조건 설정
2.2 초기 공정 조건에 따른 압축 성형 특성 분석
3. 단섬유 강화 복합소재 압축 성형-구조 연계 해석
3.1 단섬유 배향 특성에 따른 부위별 등가 이방 물성
3.2 부위별 등가 이방 물성 Mapping
3.3 압축 성형-구조 연계 해석 및 수치예제 결과
4. 결 론

1. 서 론

최근 들어 다양한 산업 분야에서 탄소배출 감소 및 RE100 등과 같은 국제적인 친환경 규제 정책이 강화되고 있으며, 전기차 및 드론 등으로 대표되는 미래 모빌리티의 경우 고효율화 달성 여부가 중요한 문제가 되었다. 이에 따라 현재 모빌리티 산업 분야에서는 고효율화 달성을 위한 다각적인 연구 개발이 진행되어 오고 있으며, 소재의 측면에서 고강도 경량 특성 및 다기능 특성 등을 종합적으로 향상시킬 수 있는 차세대 소재 개발을 위한 연구가 주목을 받고 있는 상황이다. 섬유 강화 복합소재(CFRP: Carbon Fiber Reinforced Plastic)의 경우 서로 다른 두 가지 이상의 소재(강화재 및 플라스틱 수지)를 물리적으로 혼합함으로써 폭넓은 물성 구현이 가능하며, 특히 강화재 함량비 최적화 및 수지 특성 개선 등을 통해 설계 과정에서 요구되는 기계적 특성들을 만족시킬 수 있다는 장점이 있다. 이로 인해 미래 모빌리티 부품용 소재를 종래의 금속 소재에서 섬유강화 복합소재로 대체하기 위한 시도가 지속적으로 증가하고 있다.

섬유강화 복합소재 적용 구조물의 경우 통상적으로 진공백 성형(Vacuum Bag Molding), 필라멘트 와인딩(Filament Winding), 수지 이송 성형(Resin Transfer Molding, RTM), 사출 및 압축 성형(Injecting and Compression Molding) 등과 같은 다양한 성형 공법들을 바탕으로 제작되고 있다. 상기 성형 공법들 중 금형 내부에서 복합소재에 고온/고압을 가하여 제품을 생산하는 압축 성형 공법은 필라멘트 와인딩 및 수지 이송 성형 등과 비교하여 높은 생산성을 가지며, 균일한 품질을 구현할 수 있다는 장점이 있다. 또한, 압축 성형 공법의 경우 자동화 장비 도입이 상대적으로 용이하며, 이로 인해 비교적 간단한 조작만으로 거대하고 복잡한 제품을 생산할 수 있기 때문에 복합소재 적용 모빌리티 부품 양산화에 적합한 성형 공법이라 할 수 있다. 상기 배경에 따라 복합소재 적용 구조물 제작을 위한 압축 성형 과정에서 복합소재의 종류 및 배치, 압축 온도 및 시간, 압축력 등과 같은 주요한 공정 변수들이 최종 제품의 성형 특성에 미치는 영향을 분석하기 위한 다양한 연구들이 진행되어 왔다.

프리프레그 복합소재 압축 성형의 경우, Lee 등(2016)은 전단 방향의 물성, 마찰력, 굽힘 강성 등과 같이 프리프레그 압축 성형(PCM: Prepreg Compression Molding) 특성에 주된 영향을 미치는 물성들에 대한 평가 방안을 제시하였으며, Bae 등(2018)은 프리프레그 복합소재의 면내 압축 물성 반영 여부에 따라 압축 성형 해석 결과의 정확도가 결정됨을 확인하였다. 또한, Kwak 등(2021)은 프리프레그 압축 성형 과정에서 직물의 형태 변형 문제를 해결하기 위한 방안으로써 다단 압축 성형 방법을 제안하였으며, 실험적 검증을 통해 다단 압축 성형 공정이 섬유강화 복합소재 적용 부품의 품질을 향상시킬 수 있는 공법임을 확인하였다.

한편, 양산화의 측면에서 성형성이 우수한 단섬유 복합소재 또한 고강도 경량 부품 제작 과정에서 광범위하게 활용되고 있는 추세이다. 단섬유 복합소재 구조물의 경우 소재 유동 양상에 의해 단섬유 배향 특성이 결정되며, 결과적으로 최종 성형 제품의 부위별 거동 특성 변화를 유발할 수 있다(Kim and Kim, 2019; 2020; Kim, 2023). 이에 따라 다양한 압축 성형 과정에서의 단섬유 배향 분포 및 그에 따른 구조적 거동 특성 간의 상관 관계를 실험적/해석적으로 규명하기 위한 다양한 연구들이 제안되었다. Mohammadkhani 등(2023)은 습윤 조건 및 압축 성형 공정에 따른 단섬유 배향 특성이 PA6/유리섬유 기반 복합소재의 구조적 거동에 미치는 영향을 실험적으로 분석하였으며, Kim 등(2009)은 SMC(Sheet Molding Compound) 복합소재에 대한 압축 성형 해석을 바탕으로 부위별 강화섬유 체적비 및 배향 특성 등이 고려된 성형 제품 두께 최적화를 진행하였다. Sun 등(2022)은 대표 체적 모델(RVE: Representative Volume Element)을 바탕으로 단섬유 배향 특성에 따른 소재의 기계적 거동 변화 양상을 분석하였으며, SMC 복합소재의 피로/파손 특성을 실험적/해석적으로 검증하였다. 나아가, 전산 자원의 측면에서 압축 성형 공정에 따른 SMC 복합소재의 단섬유 배향 특성을 보다 효율적으로 예측하기 위한 방안들이 제시되었다. Meyer 등(2020)은 소재 유동에 따른 Bundle 형태의 단섬유 배향 특성 예측 방안을 제안하였으며, X-ray CT 측정 결과와의 비교/분석을 통해 초기 Charge의 배치 조건에 따라 부위별 단섬유 배향 특성이 달라질 수 있음을 확인하였다. Lim 등(2022)은 micro-CT 분석 결과를 바탕으로 Bundle 형태의 단섬유 배향이 고려된 대표 체적 모델을 도출하였으며, 이를 통해 단섬유 배향 분포가 SMC 복합소재 구조물의 거동 특성에 미치는 영향을 분석하였다.

또한, Song 등(2018)은 탄소섬유 강화 복합소재 활용 부품 제작 과정에서 다양한 초기 Charge 배치 조건들이 압축 성형 제품의 뒤틀림 특성에 미치는 영향을 분석하였으며, Jang 등(2022)은 복합소재 적용 배터리 하우징 커버를 대상으로 압축/드레이핑 성형 해석이 연계된 멀티 스케일 설계 기법을 제시하였다.

상기 선행 연구 결과들을 바탕으로 초기 Charge 배치 등과 같은 압축 성형 공정 조건들은 최종 성형 제품의 거동 특성을 결정하는 중요한 요인이며, 결과적으로 단섬유 강화 복합소재 구조물에 대한 효과적인 사전 설계를 위해서는 구조 해석 과정에서 이와 같은 성형 특성들이 반영되어야 함을 확인할 수 있다. 하지만, 언급된 선행 연구들은 압축 성형 공정 과정에서의 단섬유 배향 특성을 효과적으로 예측하기 위한 성형 해석 방안 또는 주어진 단섬유 배향 분포를 반영한 개선된 구조 해석 방안 등에 주로 초점이 맞춰져 있다. 즉, 다양한 초기 Charge 배치 조건에 의해 결정되는 복합소재 유동 특성 및 단섬유 배향 분포에 따른 최종 성형 제품의 부위별 거동 특성 변화 등을 종합적으로 고려할 수 있는 구조 설계 방안과 관련된 추가적인 연구가 필요한 상황이다. 이에 따라 본 연구에서는 압축 성형 공정을 통해 제작되는 단섬유 강화 복합소재 구조물의 부위별 거동 특성을 보다 정확하게 예측하기 위한 압축 성형-구조 연계 해석 방안을 제시하고자 하였다. 다양한 압축 성형 공정 조건들 중 단섬유 배향 분포에 주된 영향을 미치는 초기 Charge 배치 조건에 따른 부위별 거동 특성 변화 양상을 해석적으로 분석하고자 하였으며(Meyer, 2020; Song et al., 2018), 압축 성형-구조 연계 해석을 위해 아래와 같은 해석들을 순차적으로 진행하였다.

1) 단섬유 복합소재 구조물에 대한 압축 성형 해석을 바탕으로 초기 Charge 배치 조건에 따른 복합소재의 유동 특성 및 부위별 단섬유 배향 특성을 분석하고자 하였다.

2) 단섬유 배향 분포에 따른 유효 물성 변화 양상을 분석하기 위해 평균장 균질화 이론을 바탕으로 복합소재 미세 구조가 반영된 등가 이방 물성을 도출하고자 하였다.

3) 유한요소 해석 모델에 상기 도출된 부위별 등가 이방 물성을 Mapping함으로써 다양한 초기 Charge 배치 조건들이 최종 성형품의 구조적 거동 특성에 미치는 영향을 반영하고자 하였다.

수치 예제로써 사각 평판에 대한 압축 성형-구조 연계 해석을 수행하였으며, ASTM D638 규격 인장 시편 가공 위치에 따른 기계적 거동 특성 차이를 비교/분석함으로써 압축 성형 과정에서 초기 Charge의 형상 및 배치 조건이 단섬유 복합소재 구조물의 부위별 거동 특성에 미치는 영향을 확인하고자 하였다.

2. 단섬유 강화 복합소재 구조물에 대한 압축 성형 해석

단섬유 강화 복합소재 구조물에 대한 압축 성형 해석을 통해 초기 Charge의 형상 및 배치 조건에 따른 복합소재의 유동 특성 및 그에 따른 부위별 강화 섬유 배향 분포 양상을 비교/분석하고자 하였다.

2.1 압축 성형 해석을 위한 초기 조건 설정

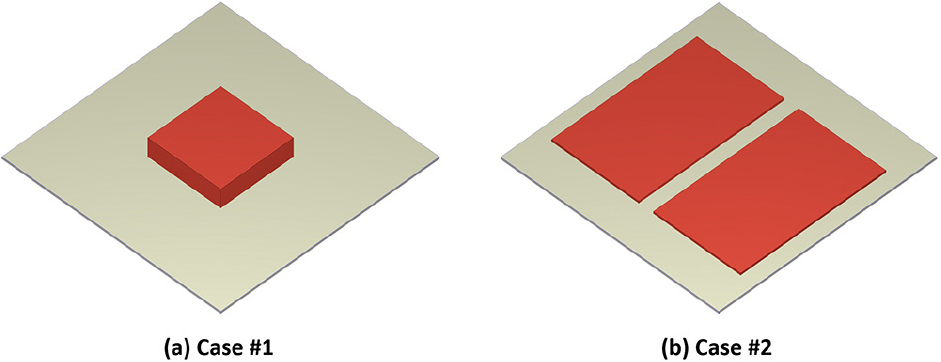
복합소재 성형 해석 S/W인 Moldex3D를 활용하여 단섬유 강화 복합소재 구조물 제작 과정에서의 압축 성형 해석을 진행하였다. 본 연구에서는 크기가 300mm × 300mm × 3mm(너비 × 길이 × 두께)인 사각 평판에 대한 압축 성형을 가정하였으며, 압축 온도 및 시간, 압축력 등과 같은 다양한 압축 성형 공정 조건들 중 단섬유 배향 분포에 주된 영향을 미칠 수 있는 초기 Charge의 형상 및 배치 조건에 따른 압축 성형 특성 변화를 분석하고자 하였다. 압축 성형 과정에서 소재 유동 특성에 따른 단섬유 배향 분포를 비교/분석하기 위해 초기 Charge의 형상 및 배치 조건을 Fig. 1과 같이 가정하였으며, 크기가 100mm × 100mm × 29mm인 직방형 charge 1개를 중앙 배치한 경우(Case #1) 및 크기가 120mm × 200mm × 6mm인 직방형 charge 2개를 대칭 배치한 경우(Case #2)를 고려하였다. 반면, 압축 온도 및 시간, 압축력 등과 같은 공정 변수들은 고정 조건들로 가정하였으며, 각각에 대한 정량적인 수치들은 Table 1과 같이 주어진다. 또한, 본 연구에서 고려되는 복합소재는 KOLON PLASTICS 社에서 제작되는 KOPA KN133G30로써, PA6 모재에 유리섬유가 30wt% 비율로 강화된 단섬유 복합소재를 가정하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F1.jpg

Fig. 1.

Initial charge conditions

Table 1.

Compression molding analysis process variables

Compression time (sec)	Maximum compression speed (mm/sec)	Maximum compression force (tf)	Melt temperature (°C)	Mold temperature (°C)
30	10	50	250	70

2.2 초기 공정 조건에 따른 압축 성형 특성 분석

2.2.1 초기 Charge 형상/배치에 따른 소재 유동 특성

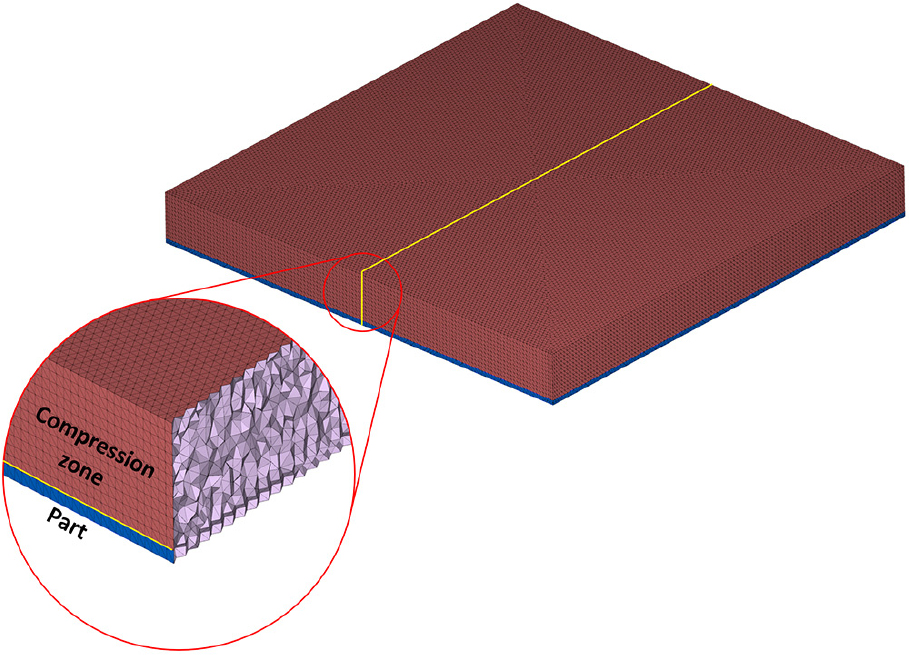
유한체적법(FVM: Finite Volume Method)을 활용하여 초기 Charge의 형상 및 배치 조건에 따른 소재 유동 특성을 분석하고자 하였다. 또한, 성형 해석 결과의 수렴성 및 계산 효율성 등을 종합적으로 고려하여 Fig. 2와 같이 이산화 과정에서 총 1,234,888개의 사면체 셀 요소를 가정하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F2.jpg

Fig. 2.

Discretization: compression zone and part

압축 성형 해석 과정에서 단섬유 복합소재의 유동은 과도/비등온 상태의 점성 유동으로 가정되며, 유동 특성을 정의하기 위한 질량, 운동량 및 에너지 보존 지배 방정식은 식 (1), (2), (3)과 같이 주어진다(Tseng et al., 2017).

(1)

\frac{\partial ρ}{\partial t} + \nabla ∙ (ρ V) = 0

(2)

ρ \frac{D V}{D t} = - \nabla P - \nabla \cdot σ + ρ g = 0

(3)

ρ C_{P} (\frac{\partial T}{\partial t} + V \cdot \nabla T) = \nabla \cdot (k \nabla T) + η {\dot{γ}}^{2}

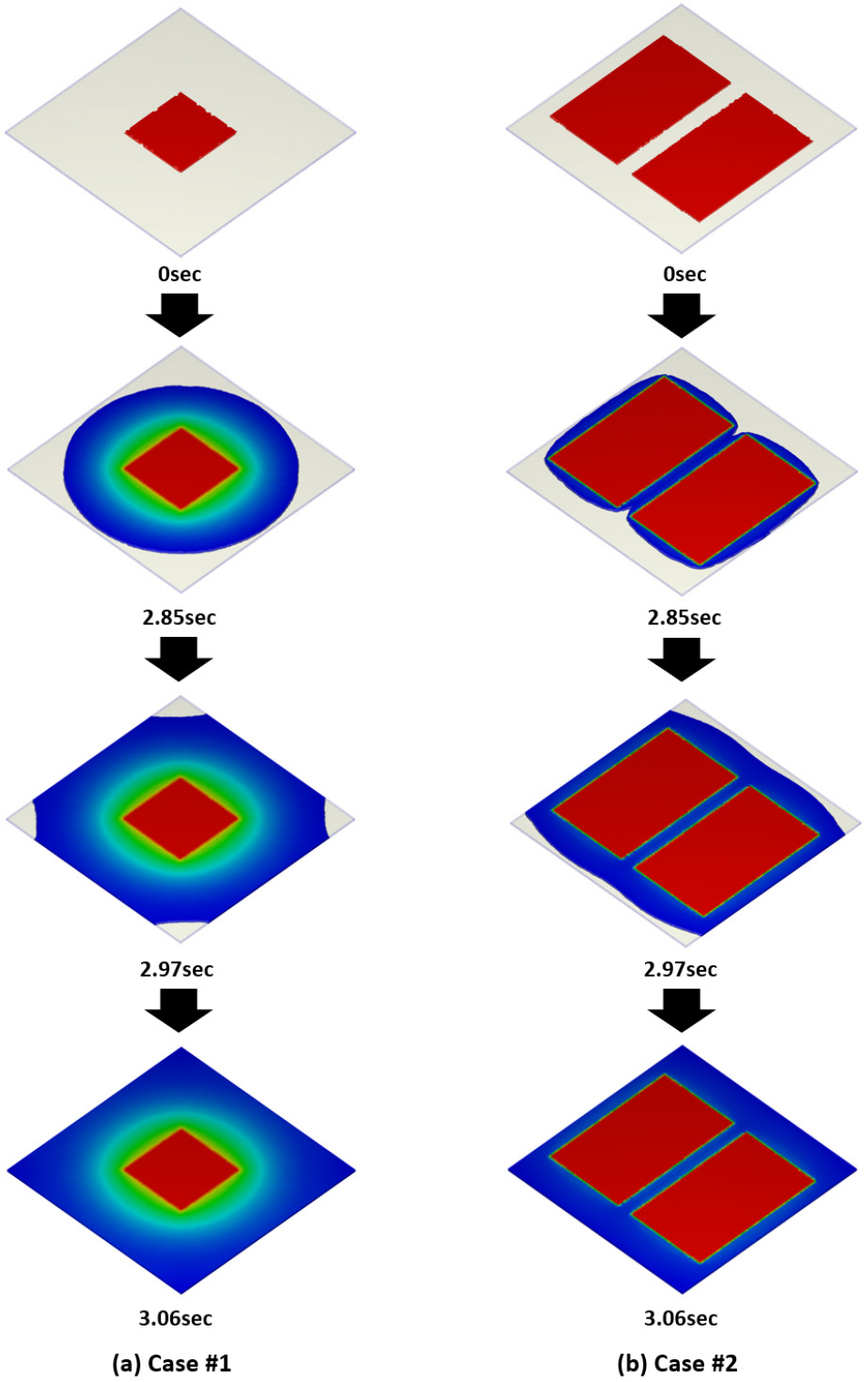
여기서, 𝜌와 $p$ 는 유체에 대한 밀도 및 압력을 나타내며, 𝜎, V 및 g는 응력 텐서, 속도 및 중력 가속도 벡터를 나타낸다. 또한, $C_{P}$ , $T$ , $k$ , 𝜂 및 $\dot{γ}$ 는 각각 비열, 온도, 열전도 계수, 점성 및 전단율을 의미한다. 상기 압축 성형 해석을 바탕으로 도출된 초기 Charge의 형상 및 배치 조건에 따른 단섬유 복합소재의 유동 특성은 Fig. 3과 같이 주어진다. Fig. 3을 바탕으로 압축 성형 공정을 활용한 부품 제작 과정에서 초기 Charge의 형상 및 배치 조건은 복합소재 유동 특성에 주된 영향을 미치는 중요한 공정 변수임을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F3.jpg

Fig. 3.

Resin flow characteristics according to the initial charge conditions

2.2.2 초기 Charge 형상/배치에 따른 단섬유 배향 특성

단섬유 복합소재의 경우 단일소재와는 대조적으로 상기 도출된 압축 성형 과정에서의 소재 유동 양상에 따라 단섬유의 배향이 부위별로 결정될 수 있다. 이에 대한 해석적 접근 방안으로써 실린더 형태의 강체 단섬유에 대한 배향 정보를 텐서의 형태로써 표현할 수 있으며, Advani-Tucker가 제안한 2차 섬유 배향 텐서(second-order orientation tensor)는 식 (4)와 같이 주어진다(Advani and Tucker, 1987).

(4)

A = \oint ψ (p) p p d p = [\begin{array}{rrr} A_{11} & A_{12} & A_{13} \\ A_{22} & A_{23} \\ Sym . & A_{33} \end{array}]

여기서, p는 단섬유 배향 특성을 나타내는 단위 벡터이며, 𝜓(p)는 각 단위 공간에서 단섬유가 존재할 수 있는 확률 분포 함수를 나타낸다. 또한, 복합소재 유동에 따른 단섬유 배향 특성은 아래와 같은 Folgar-Tucker 배향 방정식에 의해 정의될 수 있다(Folgar and Tucker, 1984).

(5)

\dot{A} = {\dot{A}}^{H D} + {\dot{A}}^{I R D}

상기 배향 방정식을 구성하는 ${\dot{A}}^{H D}$ , ${\dot{A}}^{I R D}$ 는 각각 Jeffery의 hydrodynamic(HD) 모델 및 Folgar-Tucker의 isotropic rotary diffusion(IRD) 모델을 의미하며, 이에 대한 관계식은 식 (6), (7)과 같이 주어진다(Folgar and Tucker, 1984; Jeffery, 1922; Tseng et al., 2017).

(6)

{\dot{A}}^{H D} = (W \cdot A - A \cdot W) + ξ (D \cdot A + A \cdot D - 2 A_{4} : D)

(7)

{\dot{A}}^{I R D} = 2 \dot{γ} C_{I} (I - 3 A)

식 (6)에서 W, D는 와동 텐서(vorticity tensor) 및 변형 속도 텐서(deformation rate tensor)를 나타내며, 𝜉 및 $A_{4}$ 는 단섬유 형상 인자(fiber shape factor) 및 4차 배향 텐서(fourth-order orientation tensor)를 나타낸다. 또한, 식 (7)에서 C_I, I는 각각 단섬유의 상호 작용 계수(short fiber interaction parameter) 및 3 × 3 단위 행렬(identity matrix)을 나타낸다. 상기 언급된 각 항들에 대한 세부적인 관계식은 식 (8), (9)과 같이 정의된다.

(8)

W = \frac{1}{2} (L - L^{T}), D = \frac{1}{2} (L + L^{T}), L = \nabla V

(9)

ξ = \frac{(a_{r}^{2} - 1)}{(a_{r}^{2} + 1)}, A_{4} = \oint ψ (p) pppp d p

여기서, $a_{r}$ 의 단섬유의 세장비를 나타낸다.

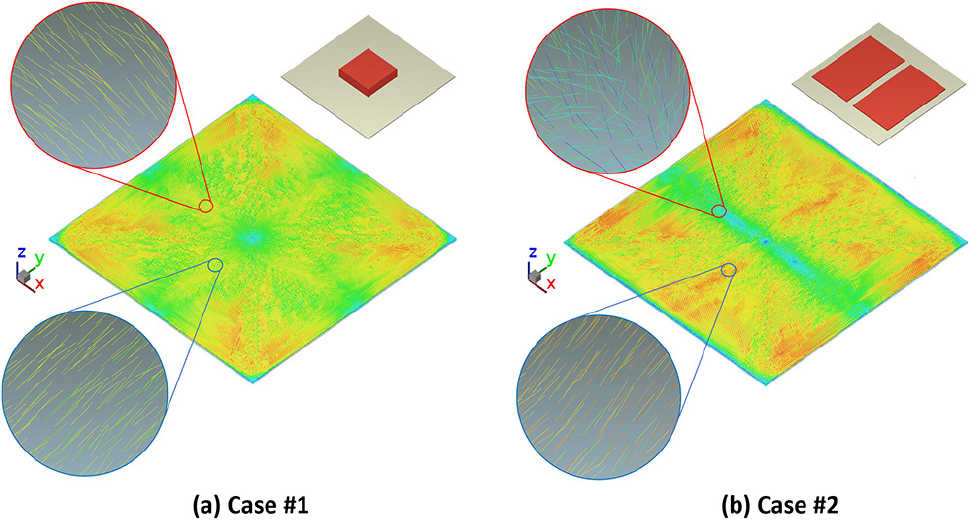
상기 관계식을 바탕으로 압축 성형 과정에서의 복합소재 유동 특성이 부위별 단섬유 배향에 미치는 영향을 분석하고자 하였으며, Fig. 4는 초기 Charge 형상 및 배치에 따른 최종 압축 성형 제품의 특정 지점에서의 단섬유 배향 특성을 나타낸다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F4.jpg

Fig. 4.

Local short-fiber orientation in specific observation points

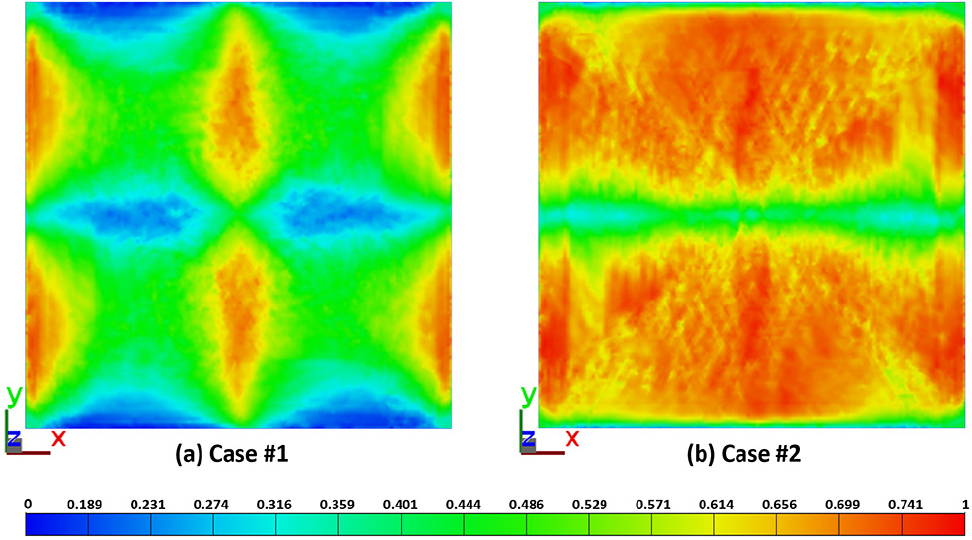
또한, 특정 기준 축을 바탕으로 도출된 최종 압축 성형 제품 전역에서의 부위별 단섬유 배향 분포는 Fig. 5와 같이 주어진다. Fig. 5에서는 기준 축을 Y 축으로 설정하였으며, 부위별 단섬유 배향 특성이 Y축과 평행/수직할 때 각각 1 및 0의 값으로 표현된다. Fig. 4 및 Fig. 5를 바탕으로 동일한 형상을 갖는 부품에 대한 압축 성형 과정임에도 초기 Charge 형상 및 배치 조건에 따라 복합소재의 유동 양상 및 그에 따른 단섬유 배향 특성이 판이해질 수 있음을 확인하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F5.jpg

Fig. 5.

Short-fiber orientation characteristics in Y direction

3. 단섬유 강화 복합소재 압축 성형-구조 연계 해석

평균장 균질화 기법을 바탕으로 부위별 단섬유 배향 특성이 반영된 등가 이방 물성을 도출한 후, 유한요소 해석 모델에 부위별 이방 물성을 Mapping함으로써 단섬유 강화 복합소재 구조물에 대한 압축 성형-구조 연계 해석을 진행하였다.

3.1 단섬유 배향 특성에 따른 부위별 등가 이방 물성

부위별 단섬유 배향 특성은 다양한 초기 공정 조건에 따른 소재 유동 양상에 의해 결정됨을 확인하였으며, 결과적으로 미시적 관점에서 최종 성형 제품의 부위별 거동 특성 변화를 유발할 수 있다. 이에 따라, 단섬유 복합소재 구조물의 기계적 거동을 정확하게 예측하기 위해서는 단섬유 배향 특성에 따른 부위별 등가 이방 물성이 구조 해석 과정에서 종합적으로 고려되어야 한다. 이를 위해 본 연구에서는 복합소재 물성 예측 S/W인 DIGIMAT-MF/MX를 활용하였으며, 평균장 균질화(mean-field homogenization) 기법을 바탕으로 단섬유 배향 특성에 따른 등가 이방 물성을 도출하고자 하였다. 단섬유 복합소재의 미시적 거동을 정의할 수 있는 대표 체적 모델(RVE: Representative Volume Element)은 식 (10)과 같이 주어진다(Kim and Kim, 2020).

(10)

\begin{aligned} ⟨ f ⟩_{ω} = v_{f} ⟨ f ⟩_{f} + v_{m} ⟨ f ⟩_{m}, \\ ⟨ f ⟩_{i} = \frac{1}{V_{i}} \int_{i} f (x) d V_{i} (i = ω, f, m) \end{aligned}

식 (10)에서 $ω$ , $f$ 및 $m$ 은 각각 대표체적모델, 강화재 및 모재의 도메인을 나타내며, $< f >_{(ω, f, m)}$ 은 각 도메인에서의 체적 평균값을 나타낸다. 또한, $V_{i}$ 는 각 도메인의 부피를 의미하며, $v_{f}$ 및 $v_{m}$ 은 강화재 및 모재의 체적비(volume fraction)을 나타낸다. 대표체적모델 및 강화재 도메인에 대한 평균 변형률 텐서는 식 (11)과 같이 주어진다.

(11)

\begin{aligned} ⟨ ϵ ⟩_{w} = v_{f} ⟨ ϵ ⟩_{f} + v_{m} ⟨ ϵ ⟩_{m}, \\ ⟨ ϵ ⟩_{f} = A^{ϵ} : ⟨ ϵ ⟩_{w} = B^{ϵ} : {⟨ ϵ ⟩}_{m} \end{aligned}

여기서, $A^{ϵ}$ 및 $B^{ϵ}$ 는 변형률 집중 텐서(strain concentration tensor)를 나타내며, 식 (12)와 같은 관계를 갖는다.

(12)

A^{ϵ} = B^{ϵ} : {[v_{f} B^{ϵ} + (1 - v_{f}) I]}^{- 1}

또한, 모재 도메인에 대한 평균 변형률 텐서를 아래와 같이 정의할 수 있다.

(13)

⟨ ϵ ⟩_{m} = {[v_{f} B^{ϵ} + (1 - v_{f}) I]}^{- 1} : ⟨ ϵ ⟩_{m}

식 (11), (12), (13)을 바탕으로 단섬유 복합소재에 대한 대표 체적 모델의 구성 방정식을 아래와 같이 정의할 수 있다.

(14)

\begin{aligned} ⟨ σ ⟩_{ω} = C_{ω} : ⟨ ϵ_{ω} ⟩, \\ C_{ω} = [v_{f} C_{f} : B^{ϵ} + (1 - v_{f}) C_{m}] : {[v_{f} B^{ϵ} + (1 - v_{f}) I]}^{- 1} \end{aligned}

상기와 같이 정의되는 평균장 균질화 및 역공학(Reverse engineering) 기법을 종합적으로 적용함으로써 도출되는 KOPA KN133G30 단섬유 복합소재의 등가 이방 물성은 Table 2와 같이 주어진다.

Table 2.

Equivalent orthotropic material properties of RVE

Young’s Modulus (MPa)	E11	10177
	E22	5571.3
	E33	5426.7
Shear Modulus (MPa)	G12	2275.2
	G13	2068.5
	G23	1837.1
Poisson’s ratio	nu12	0.39456
	nu21	0.21599
	nu13	0.38057
	nu31	0.20293
	nu23	0.49251
	nu32	0.47972

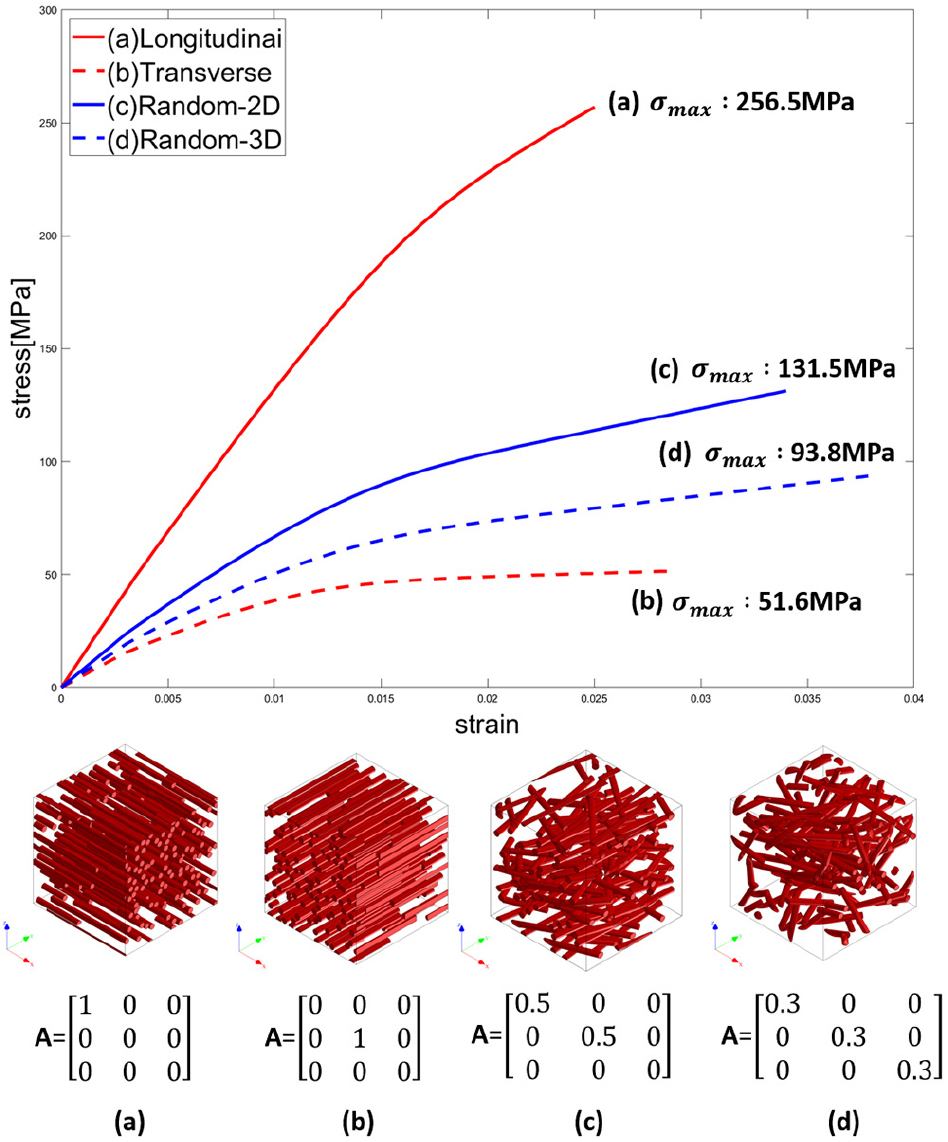
Table 2는 단섬유의 배향이 기준 축의 방향과 평행하다는 가정을 바탕으로 도출된 등가 이방 물성이며, 기준 축 방향에 대한 단섬유 배향 각도 변화에 따라 도출되는 응력-변형률 선도는 Fig. 6과 같이 주어진다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F6.jpg

Fig. 6.

Stress-Strain diagram of short-fiber reinforced composites with various fiber orientations

Fig. 6은 DIGIMAT-MX의 소재 데이터베이스에서 제공되는 응력-변형률 선도로써, KOPA KN133G30 단섬유 복합소재에 대한 인장 실험 데이터를 바탕으로 도출된 결과이다. 이를 통해 기준 축에 대한 부위별 이방 물성은 단섬유 배향 특성에 따라 결정됨을 확인하였으며, 인장 강도의 경우 배향 각도에 따라 최대 4.97배까지 차이를 나타낸다는 사실을 확인하였다. Fig. 6에서 주어지는 응력-변형률 선도들은 본 논문에서 제안하고자 하는 압축 성형-구조 연계 해석 방안의 타당성 판단을 위한 기준이 되며, 결과적으로 부위별 단섬유 배향 특성에 따른 응력-변형률 선도는 Fig. 6의 (a) 및 (b) 선도 사이의 범위에서 도출되어야 한다.

3.2 부위별 등가 이방 물성 Mapping

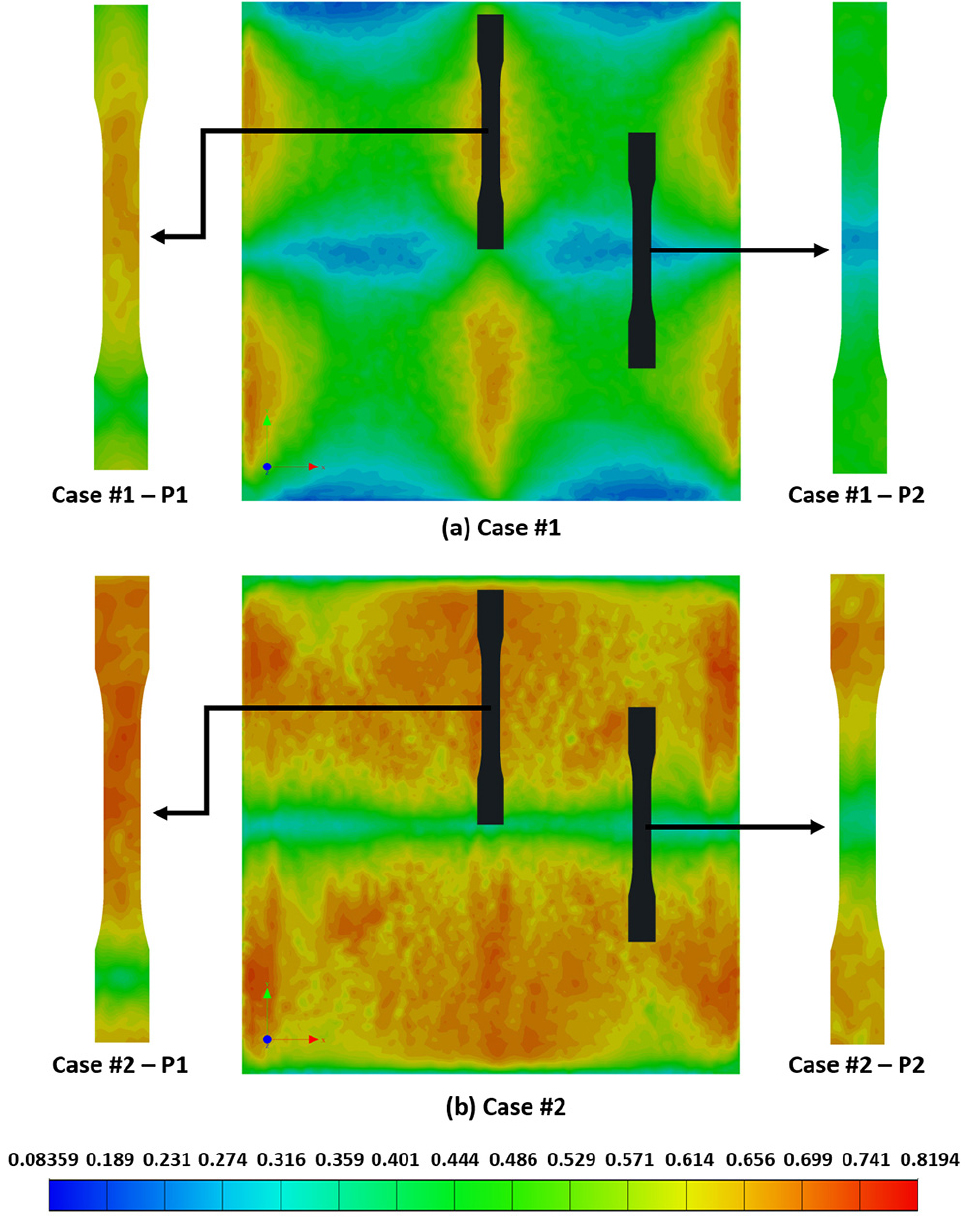
압축 성형 제품에 대한 기계적 거동을 효과적으로 예측하기 위해서는 부위별 단섬유 배향 특성에 따른 등가 이방 물성 변화 양상이 구조 해석 과정에서 반영되어야 한다. 이를 위해 DIGIMAT-MAP/RP를 활용하여 구조 해석 모델에 상기 도출된 부위별 단섬유 배향 분포 정보를 Mapping하고자 하였다. 본 연구에서는 구조 해석 모델로써 ASTM-D638 규격 인장 시편을 고려하였으며, 부위별 단섬유 배향 특성이 등가 이방 물성에 미치는 영향을 분석하기 위해 사각 평판 형태의 압축 성형 제품에서 Fig. 7과 같이 인장 시편 가공 위치를 다르게 설정하여 구조 해석을 진행하고자 하였다. Case #1 및 Case #2 사각 평판에서 P1 및 P2로 표기되는 인장 시편 가공 위치를 가정하였으며, Fig. 7은 각 인장 시편의 길이 방향을 기준으로 도출된 단섬유 배향 분포 Mapping 결과를 나타낸다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F7.jpg

Fig. 7.

Mapping of local short-fiber orientation

Fig. 7의 결과에서 단섬유 배향 특성이 인장 시편의 길이 방향과 평행/수직할 때 각각 1 및 0의 값으로 표현되며, 배향 특성이 0.4~0.6 사이의 값을 갖는 초록색 부위는 무작위 배향 특성을 나타냄을 의미한다. 이를 통해 Case #2-P1 인장 시편의 단섬유 배향 특성이 길이 방향으로 가장 명확하게 나타나며, Case #2-P2 인장 시편의 경우 게이지 구간에서 단섬유 배향 특성이 무작위로 나타나는 경향성을 확인할 수 있다. 반면, Case #1-P2 인장 시편의 경우 전체적으로는 무작위 배향 분포를 나타내지만, 시편의 길이 방향과 수직한 단섬유 배향 특성을 나타내는 중앙 부위에서 기계적 강성 저하가 예측될 수 있다. 결과적으로 Fig. 7과 같이 Mapping된 단섬유 배향 분포를 바탕으로 구조 해석 모델에 대한 부위별 등가 이방 물성을 도출할 수 있으며, 이를 바탕으로 압축 성형-구조 연계 해석을 진행할 수 있다.

3.3 압축 성형-구조 연계 해석 및 수치예제 결과

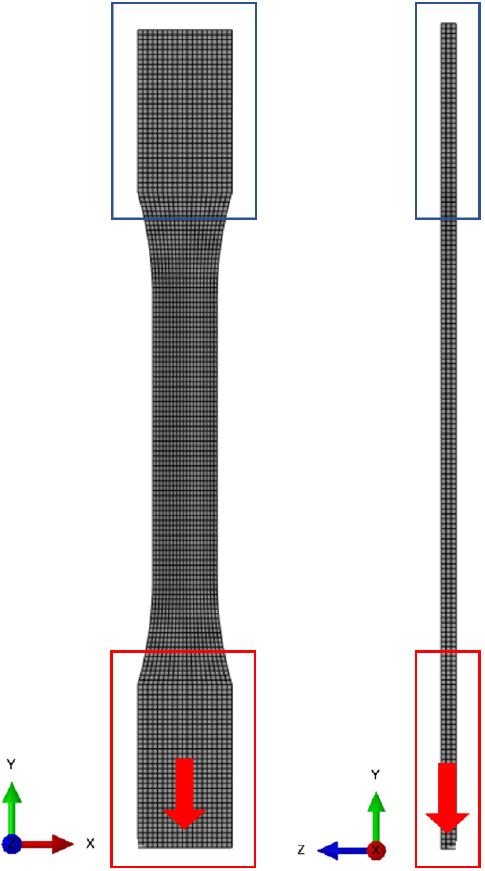
상기 부위별 단섬유 배향 정보가 Mapping된 압축 성형-구조 연계 해석을 수행하기 위해 상용 구조해석 S/W인 ABAQUS를 활용하여 인장 시편에 대한 유한요소 모델을 생성하였다. 해석 결과의 수렴성 및 계산 시간 등을 고려하여 Fig. 8과 같은 이산화 모델을 설정하였으며, 총 9,405개의 감차 적분 8절점 솔리드 요소(C3D8R element)를 가정하였다. 또한, 상기 유한요소 모델에서는 인장 시험 환경을 반영하기 위한 경계 조건을 가정하였으며, Fig. 8과 같이 한쪽 끝단을 고정하되 반대편 끝단에 시편 길이 방향으로 변위 조건을 부과하여 압축 성형-구조 연계 해석을 진행하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F8.jpg

Fig. 8.

Finite element model of tensile specimen and boundary condition

3.3.1 탄성 영역 거동 특성 분석

인장 시편의 가공 위치에 따른 선형 탄성 거동 특성 변화를 비교/분석하기 위해 Fig. 8의 이동 그립 부위의 변위를 0.5mm로 설정하여 구조 해석을 진행하였다.

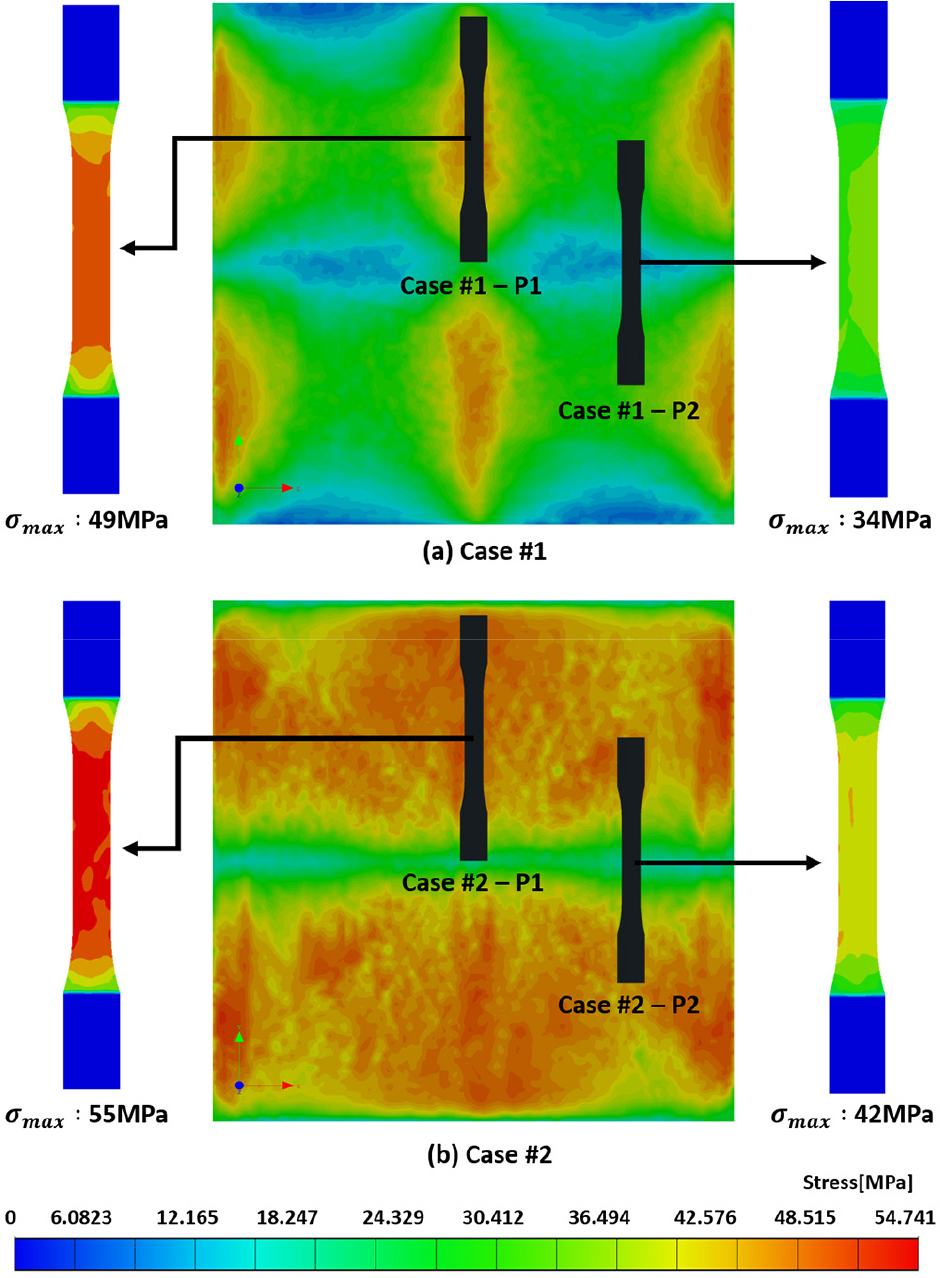
초기 Charge 조건(Case #1 및 Case #2) 및 인장 시편 가공 위치에 따른 선형 탄성 거동 특성은 Fig. 9와 같이 주어진다. 동일한 변형을 기준으로 도출된 최대 응력 수치들을 Fig. 9에서 확인할 수 있으며, 이를 통해 선형 탄성 영역에서의 각 시편의 기계적 강성 변화 양상을 도출하고자 하였다. 결과적으로 인장 시편의 길이 방향으로 단섬유 배향 특성이 지배적인 Case #2-P1 인장 시편의 경우 다른 시편들과 비교하여 가장 우수한 기계적 강성을 나타낸다는 사실을 확인할 수 있다. 반면, 시편의 중앙 부위에서 길이 방향과 수직한 단섬유 배향을 포함하는 Case #1-P2 인장 시편은 상대적으로 가장 낮은 기계적 강성을 도출한다는 사실을 확인하였다. 각 시편에 대한 최대 응력 수치들은 Case #2-P1 > Case #1-P1 > Case #2-P2 > Case #1-P2의 순서로 도출되었으며, 이러한 경향성은 Fig. 7에서 주어진 각 시편에서의 단섬유 배향 특성과 일치함을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F9.jpg

Fig. 9.

Linear elastic behavior of tensile specimens according to Initial charge conditions and positions

또한, Table 3을 통해 압축 성형 공정을 통해 제작된 사각 평판에서의 내부 위치에 따른 기계적 강성 차이를 정량적으로 분석하고자 하였다.

Table 3.

Difference of maximum stress: linear elastic analysis

Initial Charge Condition	Position #1 (P1)	Position #2 (P2)	$\frac{σ_{\max} at P 1}{σ_{\max} at P 2}$
Case #1	49MPa	34MPa	1.44
Case #2	55MPa	42MPa	1.31

Table 3의 결과를 바탕으로 Case #1 및 Case #2 사각 평판 모두 내부 위치에 따라 기계적 거동 특성 차이가 유발될 수 있으며, 또한 방사형으로 단섬유 복합소재 유동이 발생되는 Case #1의 경우 내부 위치에 따른 기계적 거동 차이가 보다 명확해짐을 확인하였다.

3.3.2 소성 영역 거동 및 파단 특성 분석

추가적으로 인장 강도 및 파단 특성 등과 같은 각 인장 시편에 대한 소성 거동 특성을 비교/분석하였으며, 해당 과정에서 ABAQUS-dynamic/explicit solver를 활용하였다.

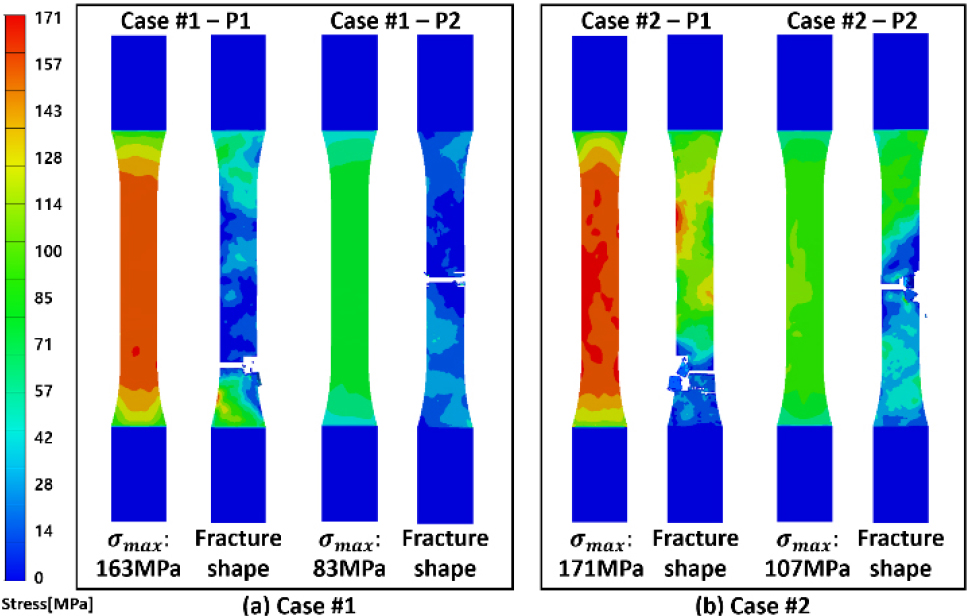
Fig. 10은 파단 발생 시점에서의 각 시편에 대한 인장 강도 및 파단 특성을 나타낸다. 파단 시 발생되는 인장 강도의 경우, 선형 탄성 거동과 유사하게 Case #2-P1 > Case #1-P1 > Case #2-P2 > Case #1-P2의 순으로 최대 응력 수치가 도출됨을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F10.jpg

Fig. 10.

Plastic behavior and fracture characteristics of tensile specimens according to Initial charge conditions and positions

또한, Case #1 및 Case #2 사각 평판에서의 내부 위치에 따른 인장 강도의 차이는 Table 4를 통해 주어지며, 선형 탄성 거동과 비교하여 내부 위치에 따른 정량적인 거동 특성 차이가 증가되는 것을 확인할 수 있다. 파단 형상의 경우, Case #1-P2 인장 시편은 중앙 부위에서의 단섬유 배향 특성으로 인해 상대적으로 파단면이 일정하게 도출된다는 사실을 확인하였다.

Table 4.

Difference of maximum stress: plastic analysis

Initial Charge Condition	Position #1 (P1)	Position #2 (P2)	$\frac{σ_{\max} at P 1}{σ_{\max} at P 2}$
Case #1	163MPa	83MPa	1.96
Case #2	171MPa	107MPa	1.59

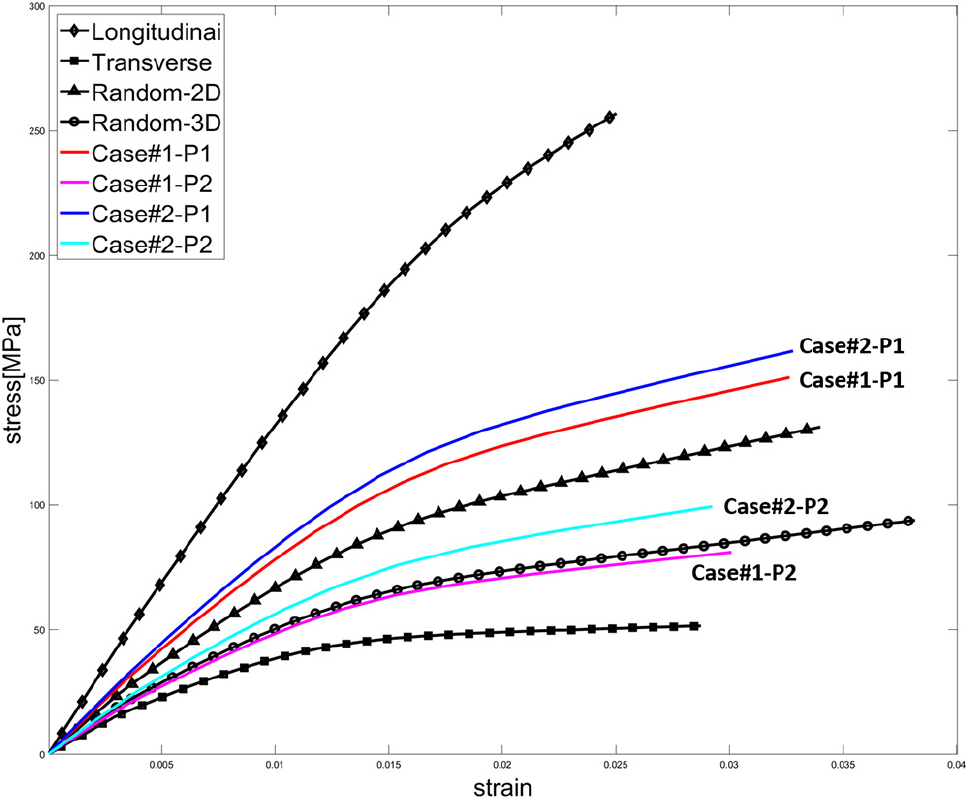
또한, Fig. 11은 각 시편에 대한 응력-변형률 선도를 나타낸다. 실험적 데이터를 바탕으로 제공되는 KOPA KN133G30 단섬유 복합소재의 응력-변형률 선도 결과들을 기준 결과로써 고려하였으며, 단섬유 배향 특성이 시편의 길이 방향에 평행(Longitudinal)/수직(Transverse)한 경우를 각각 응력-변형률 선도의 상한/하한으로 판단할 수 있다. 본 논문을 통해 해석적으로 도출된 응력-변형률 선도들은 모두 KOPA KN133G30 단섬유 복합소재에 대한 응력-변형률 선도 범위를 만족시키며, 각 인장 시편의 응력-변형률 선도 변화 양상은 인장 시편 가공 위치에 따른 단섬유 배향 분포 특성을 반영한다는 사실을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370504/images/Figure_jcoseik_37_05_04_F11.jpg

Fig. 11.

Stress-strain curve of tensile specimens according to Initial charge conditions and positions

상기 수치 예제 결과들을 바탕으로 최종 압축 성형 제품에 대한 국부적 거동 특성은 초기 Charge의 형상/배치 등과 같은 공정 조건들에 의해 결정됨을 확인하였으며, 이에 따라 압축 성형 공정을 통해 제작되는 단섬유 복합소재 구조물에 대한 정확한 사전 설계를 위해서는 압축 성형-구조 연계 해석 기법 적용이 필요하다는 사실을 확인하였다.

4. 결 론

본 연구를 통해 초기 Charge의 형상 및 배치 조건들이 최종 압축 성형 제품의 기계적 거동 특성에 미치는 영향들을 종합적으로 고려할 수 있는 압축 성형-구조 연계 해석 방안을 제시하고자 하였다. 이를 위해 압축 성형 해석을 바탕으로 초기 Charge의 형상/배치 조건에 따른 단섬유 복합소재의 유동 양상 및 부위별 단섬유 배향 특성을 분석하고자 하였으며, 평균장 균질화 이론 및 역공학 기법 적용을 통해 단섬유 배향 특성에 따른 부위별 등가 이방 물성을 도출하고자 하였다. 나아가, 부위별 단섬유 배향 정보가 Mapping된 유한요소 모델을 바탕으로 구조 해석을 수행함으로써, 초기 Charge의 형상/배치 조건에 의해 결정되는 부위별 거동 특성 변화를 효과적으로 반영할 수 있는 압축 성형-구조 연계 해석을 진행하고자 하였다.

수치 예제로써 사각 평판에 대한 압축 성형-구조 연계 해석을 수행하였으며, 최종 성형 제품에서 발생되는 부위별 거동 특성 변화를 정량적으로 분석하기 위해 가공 위치에 따른 ASTM D638 규격 인장 시편의 기계적 거동 특성을 분석하였다. 또한, 실험적 데이터를 바탕으로 도출된 응력-변형률 선도와의 비교/분석을 통해 제안된 해석 기법의 타당성을 확인하였다. 관련 수치 예제 결과 분석을 통해 동일한 형상을 갖는 압축 성형 제품임에도 초기 Charge의 형상/배치 조건에 따라 국부적 거동 특성 변화가 유발될 수 있음을 확인하였으며, 결과적으로 등방성 소재 기반 해석 방안으로는 단섬유 복합소재 구조물에 대한 정확한 설계 솔루션을 제공할 수 없음을 확인하였다. 반면, 본 논문을 통해 제안된 압축 성형-구조 연계 해석 방안은 구조물 제작 공정 과정에서 발생되는 부위별 거동 특성 변화 양상을 사전 설계 과정에서 효과적으로 반영할 수 있으며, 이를 통해 단섬유 복합소재 구조물에 대한 정확한 설계 가이드를 제시할 수 있다는 점에서 제안된 해석 방안의 필요성을 확인할 수 있다.

본 논문에서는 실험적 결과를 바탕으로 제공되는 소재 물성 데이터를 검증 과정에서 활용하였으며, 이에 따라 도출된 해석 결과에 대한 실험적 검증을 보완하기 위해 향후 복합소재 구조물 제작 및 평가와 관련된 추가적인 연구를 진행하고자 한다. 또한, 추가적인 연구로써 압축 성형 과정에서 발생될 수 있는 강화재-수지간의 상호 작용 및 잔류 응력 등을 종합적으로 고려할 수 있는 해석 방안을 제시하고자 하며, 이를 통해 단섬유 복합소재 구조물에 대한 설계 데이터의 신뢰성을 향상시킬 수 있을 것으로 기대된다.

Acknowledgements

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구이며(NRF-2022R1C1C1012599), 또한 중소벤처기업부에서 지원하는 2022년도 맞춤형 기술파트너 지원사업(RS-2022-00155265)의 연구수행으로 인한 결과물임.

References

Advani, S.G., Tucker, C.L. (1987) The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites, J. Rheol., 31(8), pp.751~784.

10.1122/1.549945

Bae, D.R., Lee, J.W., Yi, J.W., Um, M.K. (2018) Evaluation of Compression Molding Simulation with Compression Properties of Carbon Fiber Prepreg, Compos. Res., 31(6), p.421~428.

Folgar, F., Tucker, C.L. (1984) Orientation behavior of Fibers in Concentrated Suspensions, J. Reinf. Plast. & Compos., 3(2), pp.98~119.

10.1177/073168448400300201

Jang, K.S., Kim, T.R., Kim, J.H., Yun, G.J. (2022) Multi-scale Process-structural Analysis Considering the Stochastic Distribution of Material Properties in the Microstructure, Compos. Res., 35(3), pp.188~195.

Jeffery, G.B. (1922) The Motion of Ellipsoidal Particles Immersed in a Viscous Fluid, Proc. Royal Soc. London. Ser. A, Containing Papers of a Mathematical and Physical Character, 102(715), pp.161~179.

10.1098/rspa.1922.0078

Kim, M.S., Lee, W.I., Han, W.S., Vautrin, A., Park, C.H. (2009) Thickness Optimization of Composite Plates by Box's Complex Method Considering the Process and Material Parameters in Compression Molding of SMC, Compos. part A: Appl. Sci. & Manuf., 40(8), pp.1192~1198.

10.1016/j.compositesa.2009.05.003

Kim, W. (2023) Effect of Glass Fiber Orientation on Impact Fracture Properties: Coupled Injection Molding & Structural Analysis, Trans. Mater. Proc., 32(3), pp.129~135.

Kim, Y.M., Kim, Y.H. (2019) Coupled Analysis with Digimat for Realizing the Mechanical Behavior of Glass Fiber Reinforced Plastics, J. Comput. Struct. Eng. Inst. Korea, 32(6), pp.349~ 357.

10.7734/COSEIK.2019.32.6.349

Kim, Y.M., Kim, Y.H. (2020) A Study on the Fatigue Analysis of Glass Fiber Reinforced Plastics with Linear and Nonlinear Multi-Scale Material Modeling, J. Comput. Struct. Eng. Inst. Korea, 33(2), pp.81~93.

10.7734/COSEIK.2020.33.2.81

Kwak, S.H., Mun, J.H., Hong, S.H., Kwon, S.D., Kim, B.H., Kim, T.Y. (2021) Multi-stage Compression Molding Technology of Fast Curing CF/Epoxy Prepreg, Compos. Res., 34(5), pp.269~276.

Lee, J.M., Kim, B.M., Ko, D.C. (2016) CFRP Compression Forming Technology, Trans. Mater. Proc., 25(3), pp.203~208.

Lim, H.J., Choi, H., Yun, G.J. (2022) Multiscale Failure and Damage Analysis of Sheet Molding Compound (SMC) Composites using Micro-CT Image-based Reconstruction Model, Compos. Part B: Eng., 231, p.109593.

10.1016/j.compositesb.2021.109593

Meyer, N., Schöttl, L., Bretz, L., Hrymak, A.N., Kärger, L. (2020) Direct Bundle Simulation Approach for the Compression Molding Process of Sheet Molding Compound, Compos. Part A: Appl. Sci. & Manuf., 132, p.105809.

10.1016/j.compositesa.2020.105809

Mohammadkhani, P., Magliaro, J., Rahimidehgolan, F., Khapra, T., Altenhof, W. (2023) Moisture Influence on Anisotropic Mechanical behavior of Direct Compounded Compression Molded PA6/Glass LFTs, Compos. Part B: Eng., 264, p.110927.

10.1016/j.compositesb.2023.110927

Song, Y., Gandhi, U., Sekito, T., Vaidya, U.K., Vallury, S., Yang, A., Osswald, T. (2018) CAE Method for Compression Molding of Carbon Fiber-Reinforced Thermoplastic Composite using Bulk Materials, Compos. Part A: Appl. Sci. & Manuf., 114, pp.388~397.

10.1016/j.compositesa.2018.09.002

Sun, X., Li, Y., Engler-Pinto, C., Huang, L., Huang, S., Li, Z., Han, W. (2022) Characterization and Modeling of Fatigue behavior of Chopped Glass Fiber Reinforced Sheet Molding Compound (SMC) Composite, Int. J. Fatigue, 156, p.106647.

10.1016/j.ijfatigue.2021.106647

Tseng, H.C., Chang, R.Y, Hsu, C.H. (2017) Improved Fiber Orientation Predictions for Injection Molded Fiber Composites, Compos. Part A: Appl. Sci. & Manuf., 99, pp.65~75.

10.1016/j.compositesa.2017.04.004

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Prediction of the Mechanical behavior of Short-Fiber Reinforced Composite Structures using Compression Molding-Structural Coupled Analysis

ABSTRACT

MAIN

Fig. 1.

Initial charge conditions

Table 1.

Compression molding analysis process variables

Fig. 2.

Discretization: compression zone and part

(1)

(2)

(3)

Fig. 3.

Resin flow characteristics according to the initial charge conditions

(4)

(5)

(6)

(7)

(8)

(9)

Fig. 4.

Local short-fiber orientation in specific observation points

Fig. 5.

Short-fiber orientation characteristics in Y direction

(10)

(11)

(12)

(13)

(14)

Table 2.

Equivalent orthotropic material properties of RVE

Fig. 6.

Stress-Strain diagram of short-fiber reinforced composites with various fiber orientations

Fig. 7.

Mapping of local short-fiber orientation

Fig. 8.

Finite element model of tensile specimen and boundary condition

Fig. 9.

Linear elastic behavior of tensile specimens according to Initial charge conditions and positions

Table 3.

Difference of maximum stress: linear elastic analysis

Fig. 10.

Plastic behavior and fracture characteristics of tensile specimens according to Initial charge conditions and positions

Table 4.

Difference of maximum stress: plastic analysis

Fig. 11.

Stress-strain curve of tensile specimens according to Initial charge conditions and positions

Acknowledgements

References